Classes | Typedefs | Enumerations | Functions | Variables

concepts Namespace Reference

Basic namespace for Concepts-2. More...

Classes

class  _HashedSMatrix_iterator
 STL like iterator for hashed sparse matrices. More...
 
class  _Matrix_iterator
 STL iterator for matrices. More...
 
class  _Matrix_iterator_base
 Base class for STL like iterator for matrices. More...
 
class  _SubMatrix_iterator
 STL like iterator for sub matrices. More...
 
class  Absolute
 The absolute value of a element function. More...
 
class  AbsoluteComp
 The component wise absolute value of a element function. More...
 
class  AdaptiveAdjust
 Class to describe adjustments to elements in an adaptive space. More...
 
class  AdaptiveAdjustP
 Class to describe adjustments to elements in an adaptive space. More...
 
struct  AdaptiveControl
 Class to describe control structures of an adaptive space. More...
 
struct  AdaptiveControlP
 Describe control structures of a high order adaptive space. More...
 
struct  AdaptiveControlTag
 Tag information which is used in AdaptiveControl. More...
 
class  AdaptiveModel
 
class  AdaptiveQuadratureRule1d
 Adaptive quadrature rule for numerical integration. More...
 
class  AdaptiveSpace
 Abstract base class for an adaptive space. More...
 
class  Adaptivity
 Abstract base class for an adaptive classes, a.o.t. More...
 
class  AfterIteration
 Solver with after iterations. More...
 
class  AnasaziES
 
class  AnasaziMV
 
class  AnasaziOp
 
class  Array
 An array of objects. More...
 
class  ArrayCoord
 Array with coordinates of a cell. More...
 
class  ArrayCoord< 1 >
 Array with coordinates in 2D. More...
 
class  ArrayCoord< 2 >
 Array with coordinates in 2D. More...
 
class  ArrayDeterminant
 Class, which calculates the determinant for each element of the array. More...
 
class  ArrayGramMatrix
 Class, which calculates the Gram matrix M * M^T for each matrix of the array. More...
 
class  ArrayHessian
 Array of hessian matrices on quadrature points. More...
 
class  ArrayHessian< 1, 1 >
 Array of the quadratic form induced by the Hessian Matrix of the inverse transformation apllied on the tangential normal. More...
 
class  ArrayJacobian
 Array of jacobian matrices on quadrature points. More...
 
class  ArrayJacobian< 1, 1 >
 Array of jacobian determinants. More...
 
class  ArrayJacobian< 2, 2 >
 Array of jacobian matrices in 2D on 2D elements. More...
 
class  ArrayJacobian< 3, 3 >
 Array of jacobian matrices in 3D on 3D elements. More...
 
class  ArrayLocalCoord
 Array of local coordinates, e.g., inside a quad, but only along an edge. More...
 
class  ArrayMatrixInverse
 Class, which calculates the inverse matrix for each element of the array. More...
 
class  ArrayMatrixTranspose
 Class, which calculates the transpose matrix for each element of the array. More...
 
class  ArrayReciprocal
 Class, which calculates the reciprocal for each element of the array. More...
 
class  ArrayScan
 Scanner for an Array. More...
 
class  Assertion
 Exception class for assertions. More...
 
class  Attribute
 Attributes for elements of the topology. More...
 
class  AttributeBool
 A function class to query attributes. More...
 
class  AttributesFile
 
class  BaseSequence
 Sequence with operations and output operator. More...
 
class  BaseSet
 Set with operations and output operator. More...
 
class  BelosLinProb
 Decorator that decorates the Class Belos::LinearProblem<T, MV, OP> with interfaces to Concepts SparseMatrix and Vector. More...
 
class  BelosSolver
 Concepts interface to Trilinos Belos solver with different ifpack2 preconditioners and different iterative solvers. More...
 
class  BesselJ
 Class for evaluating the Bessel function of first kind. More...
 
class  BesselY
 Class for evaluating the Bessel function of second kind. More...
 
class  BiCGStab
 Solves a symmetric system of linear equations with BiConjugate Gradient Stabilized (BICGSTAB). More...
 
class  BiCGStabFabric
 Fabric class for conjugate gradients: BiCGStab. More...
 
class  BilinearF_Sum
 Sum of two bilinear forms of possible different underlying field type F. More...
 
class  BilinearF_W
 Product of scalar and a bilinear form with possible different field type F. More...
 
class  BilinearForm
 Abstract function class to evaluate a bilinear form. More...
 
class  BilinearFormContainer
 
class  BilinearFormLiCo
 A linear combination of bilinear forms. More...
 
class  BlendingHexahedron3d
 A 3D hexahedral element map for interpolation between arbitrary curved boundary quadrilateral elements according to the Linear Blending Function Method (Gordon and Hall, 1971). More...
 
class  BlendingQuad2d
 A 2D element map for a curved quadrilateral. More...
 
class  Boundary
 Class to describe an element of the boundary. More...
 
class  BoundaryConditions
 Boundary conditions. More...
 
class  BuildTColumnsBase
 Base class for classes for building T columns for elements in a space with help of space pre builder. More...
 
class  CartesianPMLFormulas
 Class for Cartesian PML. More...
 
struct  CCell_F
 Curved Cell struct that holds a physical non-vertex cell with a finite number of setted point evaluations. More...
 
struct  CCell_F_dist
 Struct that provides a CCell_F object together with a heuristic distance between given point $P$ to the finite number of physical points of the underlying cell. More...
 
class  Cell
 A cell in a mesh consist of topological information (neighbours, connectivity, orientation) and geometrical information (coordinates). More...
 
class  Cell1
 One dimensional cell. More...
 
class  Cell2
 Two dimensional cell. More...
 
class  Cell3
 Three dimensional cell. More...
 
class  CellBox
 CellBox with a specific order relation. More...
 
class  CellCondition
 
class  CellConditions
 
class  CellData
 Stores additional information on a cell, namely its father. More...
 
class  CellDiameter
 Class representing a map of diameters of elements of a given Space. More...
 
class  CellEdgeIntegral
 Integral over a edge, evaluated on a cell. More...
 
class  CellFaceIntegral
 Integral over a face, evaluated on a cell. More...
 
class  CellIntegral
 Integral, evaluated on a cell. More...
 
struct  CellMap
 Class representing a map to ElementWithCells. More...
 
class  CellPostprocess
 Abstract class for per cell postprocessing. More...
 
struct  CellStripeElement
 Cells ordered by key numbering. More...
 
class  CellToCellMapping
 
class  CellType
 
class  CellType< 1 >
 
class  CellType< 2 >
 
class  CellType< 3 >
 
class  CG
 Solves a symmetric system of linear equations with conjugate gradients (CG). More...
 
class  CGFabric
 Fabric class for conjugate gradients: CG. More...
 
class  Circle
 Mesh for a circle. More...
 
class  CircleBoundary
 
class  CircleMappingEdge2d
 2D element map for an circular arc. More...
 
class  CircleMappingEdge3d
 A 3D circular edge element map. More...
 
class  Cloneable
 Cloneable interface. More...
 
class  CmplxPart
 Abstract class for a function, which is one part of an complex function. More...
 
struct  Cmplxtype
 Taking for a real type the appropiate real type and for a real type itself. More...
 
struct  Cmplxtype< std::complex< F > >
 
class  CoeffIterator
 Iterator for an array of coefficients. More...
 
class  CoeffIterator< F, F >
 Iterator for an array of scalar coefficients. More...
 
class  CoeffIterator< F, Mapping< F, dim > >
 Iterator for an array of matrix coefficients. More...
 
class  CoeffIterator< F, Point< F, dim > >
 Iterator for an array of vector coefficients. More...
 
struct  Combtype
 Combined type. More...
 
struct  Combtype< F, std::complex< F > >
 Combined type Real * Cmplx = Cmplx. More...
 
struct  Combtype< int, F >
 Combined type int * Real = Real int * Cmplx = Cmplx. More...
 
struct  Combtype< std::complex< F >, F >
 Combined type Cmplx * Real = Cmplx. More...
 
class  ComplexFunction
 Complex function based on a real function (casting). More...
 
class  Compose
 Computes the product of two operators. More...
 
class  ComposeFormulaMatVec
 Computes the Matrix-vector product A * vf, where A is a matrix valued formula and vf a vector valued formula. More...
 
class  ComposeFormulaVecEntry
 
class  Connector
 An abstract class for elements of the topology. More...
 
class  Connector0
 A 0D element of the topology. More...
 
class  Connector1
 A 1D element of the topology. More...
 
class  Connector2
 A 2D element of the topology. More...
 
class  Connector3
 A 3D element of the topology. More...
 
class  ConnectorData
 Generalization of the class which store additional information for topological entities. More...
 
class  ConnectTwoMeshes
 Connected mesh of two given meshes where edges on both outer boundaries are connected. More...
 
class  ConstFormula
 Class for a constant formula. More...
 
class  Constrained
 Solves a linear system of equations subject to linear constraints. More...
 
class  ConvertMeshQuads
 Mesh converter. More...
 
struct  Coordinate
 
struct  CoordinateParam
 
class  Cos_n_phi
 Class for evaluating $ \cos(n\phi), n\in\mathbb{Z} $ for points $ (x,y) \in \mathbb{R}^2 $ in cartesian coordinates. More...
 
class  Cos_n_x
 Class for evaluating $ \cos(2 \pi n x/ L), n\in\mathbb{Z} $ for points $ (x,y) \in \mathbb{R}^2 $ in cartesian coordinates. More...
 
class  Cos_n_y
 Class for evaluating $ \cos(2 \pi n y/ L), n\in\mathbb{Z} $ for points $ (x,y) \in \mathbb{R}^2 $ in cartesian coordinates. More...
 
class  CRSConvertable
 Base class for operators which can be converted to Sparse Row Storage (CRS) or Sparse Column Storage (CCS) More...
 
class  Cuboid
 Concepts mesh of an cuboid $[0,a] \times [0,b] \times [0,c]$ in one hexahedron. More...
 
class  CurlHField_CircularCoil
 
class  CurvatureElementFormula
 Formula for the curvature or their derivatives on edges in 2D. More...
 
struct  Datatype
 Type of the data inside a container. More...
 
struct  Datatype< Mapping< F, DimY, DimX > >
 
struct  Datatype< Point< F, dim > >
 
class  DDSolver
 Domain Decomposition Solver. More...
 
class  DDSpace
 
class  DefFile
 
class  DenseMatrix
 Dense matrix. More...
 
class  DiagonalMatrix
 Diagonal matrix. More...
 
class  DiagonalSolver
 A solver for diagonal matrices. More...
 
class  DiagonalSolverFabric
 Fabric class for DiagonalSolver. More...
 
class  DimensionMismatch
 Exception class to express dimensions not matching. More...
 
class  Dirichlet
 Class for calculating and holding local coefficients per element which represent the dirichlet boundary condition. More...
 
class  DirichletElementFormula
 Dirichlet Data as element formula. More...
 
class  DivGradHField_CircularCoil
 
class  DomainDecomp
 Domain decomposition space. More...
 
class  DummySpace
 Space for a given dimension but without more functionality. More...
 
class  DynArray
 Container class: a dynamic array. More...
 
class  DynArrayBase
 Base class for DynArray for the non-template part. More...
 
class  DynArrayPage
 A page of a dynamic array. More...
 
class  EddyGeometry2D
 Abstract class for holding geometry and material for eddy current problems. More...
 
class  EddyGeometry2DRectImport
 Rectangular geometry, source current. More...
 
class  EddyGeometry2DRotateImport
 Geometry with rotational symmetric coil. More...
 
class  EddyGeometry2DRotational
 Rotational symmetric geometry, conductivity and source current. More...
 
class  EdgCorrFile
 
class  Edge
 An edge in the topology. More...
 
class  Edge1d
 A 1D cell: edge. More...
 
class  Edge2d
 A 1D cell: edge in 2D. More...
 
class  EdgeCoordinateChange
 Coordinate changes for edge elements. More...
 
class  EdgeCoordinateChange< 2 >
 
class  EdgeCoordinateChange< 3 >
 Coordinate changes for edge elements in a parent hexahedron. More...
 
class  EdgeData
 Stores additional information on an edge, namely its cells and faces. More...
 
class  EdgeMesh
 Base class for edge meshes. More...
 
class  EdgeNd
 A 1D cell in any dimension: edge. More...
 
class  EdgeNormalVectorRule
 Base class for defining rules in which direction the normal vector should point for created edges from quads. More...
 
class  EdgeNormalVectorRuleAttrib
 Class defining the rule that the normal vector is outwards or inwards cells with giving attribute. More...
 
class  EdgeNormalVectorRuleMidPoint
 Class defining the rule that the normal vector is outwards or inwards when looking from a given point. More...
 
class  EdgesOfVertices
 Build a mapping from vertices (over their key) in a cell to the edges their belong to. More...
 
class  EdgeTraceType
 Class EdgeTraceType holding the information about the TraceType, i.e. More...
 
class  EdgeTraceTypes
 Edge Tracetypes. More...
 
class  EdgRadiaFile
 
class  Element
 An abstract class for an element of a space. More...
 
class  ElementAndFacette
 Container for an element and one facette (edge or face). More...
 
class  ElementFormula
 Interface for a formula defined element by element. More...
 
class  ElementFormulaBoundary
 Element formula, which gives formula on the boundary. More...
 
class  ElementFormulaCompose
 
class  ElementFormulaContainer
 
class  ElementFormulaLiCo
 
class  ElementFormulaRotate2D
 Rotated element formula of a 2D vector (90� to right). More...
 
class  ElementFormulaVector
 Vectorial formula created from a FE function. More...
 
class  ElementFormulaVector< 1, F, G, H >
 Scalar formula created from a FE function. More...
 
class  ElementFormulaVectorBase
 Base class for Formula created from a FE function. More...
 
class  ElementFunction
 An abstract class for a function in a FE space. More...
 
class  ElementGraphics
 Handles graphics output (to a file) of a specific element. More...
 
class  ElementGraphicsBase
 Base class for graphics output, which holds graphics types. More...
 
class  ElementMatrix
 Element matrix. More...
 
class  ElementMatrixBase
 Base class for element matrices. More...
 
class  ElementNotInDomainOfFormula
 Exception class to express that an inquired element is not in the domain. More...
 
class  ElementPair
 Gives access to a pair of elements. More...
 
class  ElementPairList
 Holds a list of ElementPair and allows to scan over this list. More...
 
class  ElementWithCell
 Element with cell. More...
 
class  EllipseMappingEdge2d
 2D element map for an ellipsoidal arc (not skewed) More...
 
class  Estimator
 
class  ExceptionBase
 Base class for exceptions. More...
 
class  Exp_i_n_phi
 Class for evaluating $ \exp(\mathrm{i}n\phi), n\in\mathbb{Z} $ for points $ (x,y) \in \mathbb{R}^2 $ in cartesian coordinates. More...
 
class  Exp_i_n_x
 Class for evaluating $ \exp(2 \pi i n x/ L), n\in\mathbb{Z} $ for points $ (x,y) \in \mathbb{R}^2 $ in cartesian coordinates. More...
 
class  Exp_i_n_y
 Class for evaluating $ \exp(2 \pi i n y/ L), n\in\mathbb{Z} $ for points $ (x,y) \in \mathbb{R}^2 $ in cartesian coordinates. More...
 
class  ExplicitResidual
 
class  Ez4uException
 Exception class to express a problem in a ez4u input file. More...
 
class  FaceData
 Stores additional information on a face, namely its cells. More...
 
class  FaceNormalVectorRule
 Class for defining rules in which direction the normal vector should point for created faces from hexahedrons. More...
 
class  FacetteTraceType
 Class FacetteTraceType holding the information about the TraceType, i.e. More...
 
class  FacetteTraceTypes
 Facette Tracetypes. More...
 
class  FFEF_Error
 Exception class to handle errors in the FormulaFromElementFormula class. More...
 
class  File
 Base class for File type recognition. More...
 
class  FileOpenError
 Indicates that there were problems in a file open operation. More...
 
class  FluxesError
 Exception class to handle errors in the Fluxes class. More...
 
class  Flyweight
 flyweight memory manager More...
 
class  Formula
 Interface for a formula. More...
 
class  FormulaContainer
 
class  FormulaExpImag1D
 Formula for $u \mathrm{exp}(ik(x-x_0))$. More...
 
class  FormulaExpImag2D
 Formula for $u \mathrm{exp}(ik(x-x_0))$. More...
 
class  FormulaExpImag2DGrad
 Formula for gradient of a plane wave. More...
 
class  FormulaExpImag2DRadialDer
 Formula for radial derivative of $u \mathrm{exp}(ik(x-x_0))$. More...
 
class  FormulaFromElementFormula
 Projection class that allows to project an ElementFormula (i.e. More...
 
class  FormulaIncPlaneWaveSource
 Formula for $ -a \Delta u_{inc} + b k^2 u_{inc}$. More...
 
class  FormulaLayerPlaneWaveLayer
 Formula for plane wave source in layered structure. More...
 
class  FormulaLayerPlaneWaveLayerGrad
 Formula for gradient of plane wave source in layered structure. More...
 
class  FormulaLayerPlaneWaveSource
 Formula for plane wave source in layered structure. More...
 
class  FormulaLayerPlaneWaveSourceGrad
 Formula for plane wave source in layered structure. More...
 
class  FormulaLayerPlaneWaveTotal
 Formula for plane wave source in layered structure. More...
 
class  FormulaLayerPlaneWaveTotalGrad
 Formula for gradient of plane wave source in layered structure. More...
 
class  FormulaLiCo
 Linear combination of two formulae. More...
 
class  FormulaNormalOuterSP2D
 Computes the scalar product <n, vf> of the normal n with a vector valued formula vf, the result is a scalar formula in F. More...
 
class  FormulaPMLBoxRestriction
 
class  FormulaPMLCart
 Class for Cartesian PML, see Collino & Monk. More...
 
class  FormulaPMLCartNew
 New class for Cartesian PML that gets rid of the equation coefficients in the PML structure. More...
 
class  FormulaPMLEdgeRadia
 Class for radial PML in polar coordinates. More...
 
class  FormulaPMLHamburger
 Class providing the formulas for hamburger PML. More...
 
class  FormulaPMLPowerSigma
 
class  FormulaPMLPowerSigma2D
 Class for the function $\sigma(r)$ for radial PML, see INRIA report of Collino & Monk. More...
 
class  FormulaPMLPowerSigmaB2D
 Class for the function $\overline{\sigma}(r)$ for radial PML, see INRIA report of Collino & Monk. More...
 
class  FormulaPMLRadia
 Class for PML in polar coordinates. More...
 
class  FormulaSyntaxError
 Exception indication that a formula contains a syntax error reported by the parser. More...
 
class  FortranException
 Exception indicating an error in a FORTRAN routine returning a non-zero info flag. More...
 
class  Frm_Product
 Class for a product of formula. More...
 
class  Frm_Sum
 Class for a sum of formula. More...
 
class  FrmE_Component
 Class representing a component of an element formula. More...
 
class  FrmE_Component_Matrix
 Class representing a component of an element formula. More...
 
class  FrmE_Conjugate
 Conjugate complex of an element formula. More...
 
class  FrmE_Inverse
 Inverse of an element formula. More...
 
class  FrmE_NormalVector
 Element formula on 1D elements based on Edge2d returning the normal vector. More...
 
class  FrmE_NormalVector3d
 Element formula on 2D elements based on Quad3d returning the normal vector. More...
 
class  FrmE_PMLTransformation
 
class  FrmE_PointsToMapping
 
class  FrmE_PointsToMapping< 2, F, G >
 
class  FrmE_PointToMapping
 Class which maps an element formula of type Point (a vector) to one of type Mapping (a matrix). More...
 
class  FrmE_Product
 Product of two element formulas or an element formula and a factor. More...
 
class  FrmE_ScalarProductNormalEdge2d
 Computes the scalar product <n, vf> of the normal n with a vector valued formula vf, the result is a scalar formula in F. More...
 
class  FrmE_Sum
 Class for a sum of element formulas. More...
 
class  FrmE_TangentialVector
 Element formula on 1D elements based on Edge2d returning the tangential vector (left of normal vector). More...
 
class  FrmE_Trace
 
class  Function
 Abstract class for a function. More...
 
struct  GeneralMapping
 Introduction of a mapping type which is Real or Cmplx for dimension 1 and Mapping<Real,dim> or Mapping<Cmplx,dim> for higher dimensions. More...
 
struct  GeneralMapping< F, 1 >
 
struct  GeneralPoint
 Introduction of a point type which is Real or Cmplx for dimension 1 and Point<Real,dim> or Point<Cmplx,dim> for higher dimensions. More...
 
struct  getTypeOfObject
 Return the dynamic type of a polymorphic object. More...
 
class  GlobalPostprocess
 Global Postprocessing. More...
 
class  GMRes
 Solves a system of linear equations with general minimal residuals (GMRes). More...
 
class  GMResFabric
 Fabric class for generalized minimal residual: GMRes. More...
 
class  GmshInputException
 Exception class to express a problem in a gmsh (.msh) input file. More...
 
class  Graph
 Template class to define a graph. More...
 
class  GraphVertex
 Template class to define a graph vertex. More...
 
class  HamburgerPMLFormulas
 Class for hamburger PML A hamburger PML is divided in three parts one rectangle in the middle region, called "steak", two semi-circles below and above the steak, called "bread". More...
 
class  Hash
 
class  Hash< QuadratureOrder >
 
class  Hash< ShapeFunction1DOrder >
 
class  HashedSparseMatrix
 A matrix in sparse storage using hashes. More...
 
class  HashMap
 
class  Hex3dSubdiv2x
 Subdivision strategy for hexahedrons which generates 2 children. More...
 
class  Hex3dSubdiv2y
 Subdivision strategy for hexahedrons which generates 2 children. More...
 
class  Hex3dSubdiv2z
 Subdivision strategy for hexahedrons which generates 2 children. More...
 
class  Hex3dSubdiv4x
 Subdivision strategy for hexahedrons which generates 4 children. More...
 
class  Hex3dSubdiv4y
 Subdivision strategy for hexahedrons which generates 4 children. More...
 
class  Hex3dSubdiv4z
 Subdivision strategy for hexahedrons which generates 4 children. More...
 
class  Hex3dSubdiv8
 Subdivision strategy for hexahedrons which generates 8 children. More...
 
class  Hex3dSubdivision
 Interface for geometrical subdivision strategies for hexahedrons. More...
 
class  Hexahedron
 A hexahedron in the topology. More...
 
class  Hexahedron3d
 A 3D cell: hexahedron. More...
 
class  HexSubdiv2x
 Subdivision strategy for hexahedrons which generates 2 children perpendicular to the x direction. More...
 
class  HexSubdiv2y
 Subdivision strategy for hexahedrons which generates 2 children perpendicular the y direction. More...
 
class  HexSubdiv2z
 Subdivision strategy for hexahedrons which generates 2 children perpendicular to the z direction. More...
 
class  HexSubdiv4x
 Subdivision strategy for hexahedrons which generates 4 children along the x direction. More...
 
class  HexSubdiv4y
 Subdivision strategy for hexahedrons which generates 4 children along the y direction. More...
 
class  HexSubdiv4z
 Subdivision strategy for hexahedrons which generates 4 children along the z direction. More...
 
class  HexSubdiv8
 Subdivision strategy for hexahedrons which generates 8 children. More...
 
class  HexSubdivision
 Interface for topological subdivision strategies for hexahedrons. More...
 
class  HField_CircularCoil
 
class  HRefinement
 Uniform h refinement. More...
 
class  ImagPart
 Function as imaginary part of an complex function. More...
 
class  ImplicitEquilibratedA0Error
 
class  Import2dMesh
 
class  Import2dMeshBase
 Imports 2D mesh with triangles and quadrilaterals (possibly mixed). More...
 
class  Import2dMeshEz4u
 Imports 2D mesh with triangles(currently not supported) and quadrilaterals (possibly mixed) from mesh generator ez4u. More...
 
class  Import2dMeshGeneral
 
class  Import2DMeshGmsh
 Imports a 2D quadrilateral mesh from mesh generator gmsh. More...
 
class  Import3dMesh
 Imports 3D mesh with tetrahedra and hexahedra. More...
 
class  Import3DMeshGmsh
 Imports a 3D mesh consisting only of hexahedrons from created with the mesh generator gmsh. More...
 
class  Import3DTetMesh
 Importer for tetrahedral meshes in notation which was used in [1]. More...
 
class  ImportMesh
 Base class for reading a mesh from a file. More...
 
struct  Index
 Stores a number of indices in a ordered fashion. More...
 
class  IndexNotExisting
 Exception class to express that an index in a dynamic array does not exist. More...
 
struct  IndexRange
 Class for a range of global indices. More...
 
class  InfiniteEdge
 An infinite edge in the topology, which possess only one vertex as the other lies in the infinite. More...
 
class  InfiniteQuad
 A infinite quadrilateral in the topology, which possess one Edge and two InfiniteEdges since one edge lies in the infinite. More...
 
class  InfiniteQuad2d
 A 2D cell: infinite quadrilateral. More...
 
class  InfiniteRect2d
 A 2D cell: infinite rectangle. More...
 
class  InfQuadSubdiv2V
 Subdivision strategy for infinite quadrilaterals which generates two children which are infinite quadrilaterals as well. More...
 
class  InfQuadSubdivision
 Interface for topological subdivision strategies for infinite quadrilaterals. More...
 
class  InnerOuterBoundary2d
 Base class for mesh classes in 2D which defines its outer boundary and inner boundaries. More...
 
class  InnerResidual
 
class  InOutParameters
 Holds parameters in hashes. More...
 
class  InputAdaptiveModels
 Helps for reading input parameters for single solving with AdaptiveModels. More...
 
class  InputEddy2DGeometries
 Helps for reading input parameters for Eddy2D geometries. More...
 
class  InputFile
 Helps for reading the input parameter of file name. More...
 
class  InputParameter
 Abstract class for carrying information, which helps for reading input parameters from command line. More...
 
class  InputParser
 Parses an input file and extracts parameters. More...
 
class  IntegrationCell
 Cell over which can be integrated. More...
 
class  InverseMappingEdge2d
 In existant 2D element map for an edge the direction in the edge are inversed. More...
 
class  InverseVertexQuadSector2d
 A 2d inverse mapping from a sector to reference element. More...
 
class  JacobianCell
 Basic template class for a Jacobian Cell. More...
 
class  JacobianCell< 1 >
 
class  JacobianCell< 2 >
 
class  JacobianCell< 3 >
 
class  Joiner
 Joiner class with multiple successors, i.e. More...
 
class  Karniadakis
 Part of the multidimensional expansion bases for the shape functions of Karniadakis and Sherwin. More...
 
class  KarniadakisNew
 
class  Key
 Key class. More...
 
class  Laguerre
 Laguerre polynomials. More...
 
class  LaguerreBasis
 Polynomial functions which gives a basis of the semi-infinite intervals after multiplication with factor. More...
 
class  LapackChol
 Linear solver using Lapack subroutine DPOSV. More...
 
class  Legendre
 Class representing Legendre polynomials evaluated on quadrature points. More...
 
struct  Level
 Level information used for multidimensional hp FEM. More...
 
class  LiCo
 Linear combination of two operators. More...
 
class  LiCoI
 Linear combination of an operator with the identity. More...
 
class  Line
 Mesh for the interval of the real axis. More...
 
class  LinearForm
 Abstract class for a linear form. More...
 
class  LinearFormChoice
 Interface class for Linearform in that one can choice for the basis evaluation type, represented by "Basis" enum. More...
 
class  ListScan
 Scanner for a list. More...
 
class  LocalDtNmapFeng2D
 Class that allows to apply the local DtN Boundary Conditions of Feng for the Helmholtz equation for order 1-5. More...
 
class  LocalEstimator
 ‍** More...
 
struct  ltidx
 
struct  ltstr
 
class  MacroElementNode
 
class  Map1d
 An abstract class for a 1d map. More...
 
class  Map2d
 An abstract class for a 2d map. More...
 
class  Map3d
 An abstract class for a 3d map. More...
 
class  MapEdge1d
 A 1D element map for an edge. More...
 
class  MapHexahedron3d
 A 3D element map for a hexahedron. More...
 
class  MapParallelepiped3d
 A 3D element map for a Parallelepiped. More...
 
class  Mapping
 Basic class for a 2D or 3D map. More...
 
class  MappingEdge2d
 A 2D element map for an edge. More...
 
class  MappingEdge3d
 Base class for an edge element map $ F_K : [0,1] \to \mathbb{R}^3 $. More...
 
class  MappingHexahedron3d
 Interface for the element map of a hexahedron embedded in R^3 (analogous to the design of MappingQuad2d in two dimensions) More...
 
class  MappingHexahedronEdge3d
 3D element map for an edge as part of a Hexahedron. More...
 
class  MappingParallelEdge2d
 2D element map for an edge parallel to another one. More...
 
class  MappingQuad2d
 A 2D element map for a quadrilateral. More...
 
class  MappingQuadEdge2d
 2D element map for an edge as part of an quad. More...
 
class  MappingStraightEdge2d
 A 2D element map for an edge of a straight line. More...
 
class  MappingStraightEdge3d
 A 3D straight edge element map. More...
 
class  MappingTriangle2d
 A 2D element map for a triangle. More...
 
class  MapQuad2d
 A 2D element map for a quadrilateral given by a formula. More...
 
class  MapTetrahedron3d
 A 3D element map for a tetrahedron. More...
 
class  MapTriangle2d
 A 2D element map for a triangle. More...
 
class  MapTriangle3d
 A 3D element map for a triangle. More...
 
class  MatfileIO
 Concepts *.mat-file tool. More...
 
class  MatfileIOError
 Exception class to handle errors in the matfileIO class. More...
 
class  Matrix
 Abstract class for an operator. More...
 
class  MatrixElementFormula
 Element formula returning a matrix. More...
 
class  MatrixNotBuilt
 Indicates that a needed matrix wasn't build yet. More...
 
class  MaxwellBoundary
 Class for holding boundary type of Maxwell's problems. More...
 
class  MaxwellModel
 Abstract class for Maxwell's problems. More...
 
class  Mesh
 An abstract class for meshes. More...
 
class  Mesh1
 An abstract class for 1D meshes. More...
 
class  Mesh2
 An abstract class for 2D meshes. More...
 
class  Mesh2withBoundary
 Base class for mesh classes in 2D which defines its outer boundary and inner boundaries. More...
 
class  Mesh3
 An abstract class for 3D meshes. More...
 
class  MeshGraph2
 
class  MeshGraph2_Edge
 
class  MissingFeature
 Exception class to express a missing feature. More...
 
class  MissingParameter
 Indicates that a requested parameter is not present. More...
 
class  Model
 Base class for a model. More...
 
class  ModelControl
 
class  ModelControl< hp2D::Eddy2D_E >
 
class  ModelControl< hp2D::Maxwell2D_E >
 
class  ModelControl< hp2D::Maxwell2D_H >
 
class  ModelControl< hp2D::Maxwell2D_H_Base >
 
class  ModelControl< hp2D::Maxwell2D_H_DD >
 
class  ModelControlBase
 Base class for controlling a model. More...
 
class  ModelNotSolved
 Indicates that a model wasn't solved yet. More...
 
class  MultiArray
 Container typename for multidimensional Array which is based on std::map. More...
 
class  MultiArray< 1, T >
 Container typename for multidimensional Array which is based on std::map. More...
 
class  MultiEntrance
 
class  MultiEntrance< 1, T >
 
class  MultiIndex
 
class  multilevelindex
 Class for the multilevel index. More...
 
class  Multiple
 Multiple of an operator. More...
 
class  multiplies
 
class  MultiVector
 A multivector in dimension dimC with const pointer entries. More...
 
class  MultiVector< 0, concepts::Set< CellBox< 1 > > >
 
class  MultiVector< 0, concepts::Set< CellBox< 2 > > >
 
class  MultiVector< 0, concepts::Set< CellBox< 3 > > >
 
class  MultiVector< 0, const ElementWithCell< Cmplx > * >
 
class  MultiVector< 0, const ElementWithCell< Real > * >
 
class  Mumps
 MUMPS : MUltifrontal Massively Parallel sparse direct Solver. More...
 
class  MumpsException
 Exception indicating that the Mumps solver failed. More...
 
class  MumpsFabric
 Fabric class for Mumps. More...
 
class  MumpsOverlap
 MUMPS : MUltifrontal Massively Parallel sparse direct Solver. More...
 
class  MumpsOverlapFabric
 Fabric class for Mumps with overlaping. More...
 
class  MutableMesh1
 Class for holding a general mutable mesh of line elements where cells can be added. More...
 
class  MutableMesh2
 Class for holding a general mutable mesh of 2D cell where cells and other 2D meshes can be added. More...
 
class  MutableMeshBase
 Base class for mutable meshes. More...
 
class  NegativeJacobian
 Exception which indicates that a negative Jacobian was found. More...
 
class  Neumann
 Abstract class for the Neumann boundary term. More...
 
class  Newton
 Solves a non-linear system of the form A(X)=Y. More...
 
class  NewtonException
 Exception indicating that the Newton solver failed. More...
 
class  NoConvergence
 Exception indicating that the solver did not converge up to the desired accuracy in the given number of iterations. More...
 
class  NoMPIInit_Error
 Exception class to handle MPI::Init() lack of call. More...
 
class  NotValidDof
 Exception class to express that an inquired dof is not valid. More...
 
class  NRLSolver
 
struct  null_deleter
 
struct  number
 Name traits for number types. More...
 
struct  number< double >
 Name traits for the number type Real. More...
 
struct  number< hp2D::hpAdaptiveSpaceH1 >
 
struct  number< hp2D::hpAdaptiveSpaceL2 >
 
struct  number< long double >
 Name traits for the number type Real. More...
 
struct  number< Mapping< F, dim > >
 
struct  number< Point< F, dim > >
 
struct  number< std::complex< double > >
 Name traits for the number type Cmplx. More...
 
struct  number< std::complex< long double > >
 Name traits for the number type Cmplx. More...
 
class  OpAdd
 
class  Operation
 
class  Operator
 Abstract class for an operator. More...
 
class  OpMult
 
class  OpRecipr
 
class  Orders
 Class combining polynomial order and number of quadrature points. More...
 
class  OrdersBase
 Class containing number of quadrature points. More...
 
class  OutputMatlab
 Class for output of objects to matlab. More...
 
class  OutputMatlab< Array< F > >
 Specialisation of class OutputMatlab<F> for output of objects to matlab to Array<F> More...
 
class  OutputMatlab< bool >
 
class  OutputMatlab< char * >
 Class for output of C strings. More...
 
class  OutputMatlab< F * >
 Class for output of pointers to matlab. More...
 
class  OutputMatlab< Mapping< F, dim > >
 Class for output of 2D and 3D matrices to matlab. More...
 
class  OutputMatlab< Point< F, dim > >
 Class for output of 2D and 3D vectors to matlab. More...
 
class  OutputMatlab< Sequence< F > >
 Specialisation of class OutputMatlab<F> for output of objects to matlab to Sequence<F> More...
 
class  OutputMatlab< std::map< F, G > >
 
class  OutputMatlab< std::queue< F > >
 
class  OutputMatlab< std::set< F > >
 
class  OutputMatlab< std::string >
 Class for output of C++ strings. More...
 
class  OutputMatlab< std::vector< F > >
 
class  OutputMatlab< StiffArray< dim, F > >
 Specialisation of class OutputMatlab<F> for output of objects to matlab to StiffArray<dim,F> More...
 
class  OutputOperator
 Class providing an output operator. More...
 
class  OutputTecplot
 Class for output of objects to tecplot. More...
 
class  OutputTecplot< Array< F > >
 
class  OutputTecplot< Point< F, dim > >
 Class for output of 2D and 3D vectors to matlab
More...
 
class  OutputTecplot< std::complex< F > >
 
class  ParabelMappingEdge2d
 2D element map for an parabel arc. More...
 
class  Parallelepiped3d
 A 3D cell: parallelepiped. More...
 
class  Pardiso
 Sparse direct solver for symmetric and unsymmetric matrices. More...
 
class  PardisoFabric
 Fabric class for Pardiso. More...
 
class  ParsedFormula
 
class  ParsedFormula< Cmplx >
 
class  ParsedFormula< Real >
 
class  ParsedFormula< Real2d >
 
class  ParsedFormulaBase
 Parses the given string and evaluates it on request. More...
 
class  ParseObjectFromString
 Class for parsing objects like "Circle(1.0)" or "Edge(1,2)" from a string. More...
 
class  PartMappingEdge2d
 Part of a edge mapping. More...
 
class  PartMappingHexahedron3d
 A 3D element map for a restriction of a given hexahedron element mapping. More...
 
class  PartMappingQuad2d
 Part of a map of a quadrilateral. More...
 
class  Permutation
 Permutation operator. More...
 
class  PETSc
 Interface to the iterative solvers of the PETSc library. More...
 
class  PETScFabric
 Fabric class for PETSc solvers. More...
 
class  PETScMat
 Interface to the sparse matrices from PETSc. More...
 
class  PiecewiseConstDynArrayFormula
 Piecewise constant function defined by attributes, base on dynamic array. More...
 
class  PiecewiseConstFormula
 Piecewise constant function defined by the attribute of a cell. More...
 
class  PiecewiseConstImportFormula
 Piecewise constant function defined by attributes, imported from a file. More...
 
class  PiecewiseElementFormula
 Piecewise defined function defined by attributes. More...
 
class  PiecewiseFormula
 Piecewise defined function defined by attributes. More...
 
class  PiecewiseFormula0
 Piecewise defined function, which consists of a formula and a default value. More...
 
class  PiecewiseFormulaBase
 Piecewise defined function on a number of cells. More...
 
class  PiecewiseFormulaCombine
 Combines two piecewise defined formulas with an operation, e.g. More...
 
class  PiecewiseFormulaFun
 Piecewise defined function as an analytical function of another piecewiese defined function. More...
 
class  PiecewiseFormulaVector
 
class  PiecewiseFormulaVector< 1, F, G, H >
 
class  PiecewiseFormulaVectorBase
 Base class for piecewise defined formula, which are a function of a FE function. More...
 
class  PListScan
 Scanner for a list of pointers. More...
 
class  Point
 Basic class for a Point or a vector. More...
 
class  PointerToEmptyBilinearForm
 Exception class to express that the RCP pointer points to 0. More...
 
class  PointerToEmptyElementFormula
 Exception class to express that the RCP pointer points to 0. More...
 
class  PointerToEmptyFormula
 Exception class to express that the RCP pointer points to 0. More...
 
class  PointInCell
 Define a point inside a geometrical cell by its connector and the coordinate in the reference cell. More...
 
class  PointInCell< 1 >
 
class  Pool
 Pool for blockwise memory allocation. More...
 
class  PrecondSolverFabric
 Abstract fabric class for linear solvers with preconditoner. More...
 
class  PRefinement
 Uniform p refinement. More...
 
class  ProcessParameter
 Reads command line. More...
 
class  PStlVectorScan
 Scanner for a STL container std::vector of pointers. More...
 
class  QR_Q
 Gives min(N,M) by min(N,M) - Q matrix of QR decomposition of a M by N non sparse matrix A. More...
 
class  Quad
 A quadrilateral in the topology. More...
 
class  Quad2d
 A 2D cell: quadrilateral. More...
 
class  Quad2dSubdiv2H
 Subdivision strategy for quadrilaterals which generates two children. More...
 
class  Quad2dSubdiv2V
 Subdivision strategy for quadrilaterals which generates two children. More...
 
class  Quad2dSubdiv4
 Subdivision strategy for quadrilaterals which generates four children. More...
 
class  Quad2dSubdivision
 Interface for geometrical subdivision strategies for quadrilaterals. More...
 
class  Quad3d
 A quadrilateral cell in 3D. More...
 
class  QuadCoordinateChange
 Coordinate changes for quadrilateral elements. More...
 
class  QuadCoordinateChange< 3 >
 Coordinate changes for quadrilateral face elements in a parent hexahedron. More...
 
class  QuadNd
 Base class for a quadrilateral in any dimension. More...
 
class  Quadrature
 Basic class for numerical integration. More...
 
class  QuadratureOrder
 
class  QuadratureRule
 Abtract class for quadrature rules in $ \mathbb{R}^n $. More...
 
class  QuadratureRule1d
 Quadrature rule for numerical integration. More...
 
class  QuadratureRule1dDynamic
 Base class for quadrature rules with dynamically allocated storage for the weights and abscissas. More...
 
class  QuadratureRule1dGaussJacobi
 Gauss Jacobi quadrature rule not including both endpoints. More...
 
class  QuadratureRule1dGaussLobatto
 Gauss Lobatto quadrature rule including both endpoints. More...
 
class  QuadratureRule1dTrapeze
 
class  QuadratureRule2d
 Abstract class for quadrature rules in. More...
 
class  QuadratureRule2dQuadDuffy
 Class representing the Generalized Duffy quadrature rule in 2d, $ x = u^\beta, y = u^\beta v $, that is for $ \beta=1 $ the standard duffy integration rule. More...
 
class  QuadratureRule2dQuadTensor
 Tensor quadrature rule in 2d. More...
 
class  QuadRuleFactory
 Class for creation of a quadrature rule. More...
 
class  QuadRuleFactoryBase2d
 Abstract class for quadrature rule factories in 2D. More...
 
class  QuadRuleFactoryTensor2d
 This class is the same as QuadRuleFactory, but returning integration rules in 2d. More...
 
class  QuadRuleFactoryTensorDuffy2d
 Class representing a quadrature factory, that holds information about cells on which generalized duffy quadrature should be applied. More...
 
class  QuadSubdiv2H
 Subdivision strategy for quadrilaterals which generates two children. More...
 
class  QuadSubdiv2V
 Subdivision strategy for quadrilaterals which generates two children. More...
 
class  QuadSubdiv4
 Subdivision strategy for quadrilaterals which generates four children. More...
 
class  QuadSubdivision
 Interface for topological subdivision strategies for quadrilaterals. More...
 
class  RadialPML_2D
 Class for providing the formulas in bilinear forms coming from the PML transformation of the radial PML (in 2D). More...
 
class  RadialPMLFormulas
 Class for providing the formulas in bilinear forms coming from the PML transformation of the radial PML (in 2D). More...
 
class  RCP
 Reference-counting pointer. More...
 
class  RCP< const ElementFormula< F, G > >
 
class  RCP< const Formula< F > >
 
class  RealPart
 Function as real part of an complex function. More...
 
struct  Realtype
 Taking for a complex type the appropiate real type and for a real type itself. More...
 
struct  Realtype< Array< F > >
 
struct  Realtype< Mapping< F, DimY, DimX > >
 
struct  Realtype< Point< F, dim > >
 
struct  Realtype< std::complex< F > >
 
class  RelativeCells
 Class which holds information about the mesh hierarchy and how the point in the reference cell changes from level to level. More...
 
class  ResourceMonitor
 Timer and resource monitor. More...
 
class  RestrictionSpace
 Classes for restriction of spaces to a sub-domain. More...
 
class  ResultsTable
 Organizes the results in the hashes from InOutParameters in a nice table. More...
 
class  Rys
 Rys shape function basis over an element [a,b]. More...
 
class  Scan
 An abstract class for scanning a mesh (a set of cells) or a space (a set of elements). More...
 
class  Scan< Cell1 >
 A scanner for a 1D mesh. More...
 
class  Scan< Cell2 >
 A scanner for a 2D mesh. More...
 
class  Scan< Cell3 >
 A scanner for a 3D mesh. More...
 
class  Scan< Connector0 >
 A scanner for 0D connectors on the processor intersection (cap) More...
 
class  Scan< Connector1 >
 A scanner for 1D connectors on the processor intersection (cap) More...
 
class  Scan< Connector2 >
 A scanner for 2D connectors on the processor intersection (cap) More...
 
class  Scan< constraints::Element< F > >
 
class  Scan< ElementWithCell< F > >
 
class  Scan< hp1D::BaseElement< F > >
 Scanner of hp1D::Element. More...
 
class  Scan< hp2D::Element< F > >
 Scanner of hp2D::Element. More...
 
class  Scan< hp3D::Element< Real > >
 
class  Scan< linDG3D::FvdgElement >
 Scanner over tetrahedral elements in FV/DG-space. More...
 
class  Scan< linearFEM::Element >
 
class  Scan< linearFEM::Line >
 
class  Scan< linearFEM::Quad >
 
class  Scan< linearFEM::Tetrahedron >
 
class  Scan< linearFEM::Triangle >
 
class  Scan< vectorial::Element< F > >
 
class  Scan< vectorial::ElementWithCell< F > >
 
class  SchurCompl
 Schur complement. More...
 
class  Semantics
 An abstract function class to query attributes. More...
 
class  Sequence
 Sequence with operations, output operator, and method of the particular element types. More...
 
class  Sequence< bool >
 
class  Sequence< Connector0 * >
 
class  Sequence< Connector1 * >
 
class  Sequence< Connector2 * >
 
class  Sequence< const Connector0 * >
 
class  Sequence< const Connector1 * >
 
class  Sequence< const Connector2 * >
 
class  Sequence< const Key * >
 
class  Set
 Set with operations, output operator, and method of the particular element types. More...
 
class  Set< Attribute >
 
class  Set< Connector * >
 
class  Set< Connector0 * >
 
class  Set< Connector1 * >
 
class  Set< Connector2 * >
 
class  Set< const Connector * >
 
class  Set< const Connector0 * >
 
class  Set< const Connector1 * >
 
class  Set< const Connector2 * >
 
class  Set< const Key * >
 
class  Set< IndexRange >
 
class  ShapeFunction1D
 Abstract class for 1D shape function. More...
 
class  ShapeFunction1DOrder
 
class  SharedJacobianAdj
 Shared data for bilinear forms on vectorial spaces, like hp2D::RotRot and hp2D::DivDiv. More...
 
class  SharedJacobianDet
 Shared data for bilinear forms on vectorial spaces, like Identity. More...
 
class  ShiftAndInvertOperatorForGEVPs
 
class  Sin_n_phi
 Class for evaluating $ \sin(n\phi), n\in\mathbb{Z} $ for points $ (x,y) \in \mathbb{R}^2 $ in cartesian coordinates. More...
 
class  Sin_n_x
 Class for evaluating $ \sin(2 \pi n x/ L), n\in\mathbb{Z} $ for points $ (x,y) \in \mathbb{R}^2 $ in cartesian coordinates. More...
 
class  Sin_n_y
 Class for evaluating $ \sin(2 \pi n y/ L), n\in\mathbb{Z} $ for points $ (x,y) \in \mathbb{R}^2 $ in cartesian coordinates. More...
 
class  SingletonScan
 A scanner over a single element. More...
 
class  SMatrix1D
 One dimensional S matrix. More...
 
class  SMatrixBase
 An abstract class for an S matrix. More...
 
class  SMatrixBlock
 S matrix in block form for tensorised shape functions. More...
 
class  SMatrixCompose
 Composing S matrices. More...
 
class  SMatrixGeneralTensor
 S matrix for elements in dimensions 2 and 3 with tensorized shape functions, with arbitrary number of shape functions in each direction. More...
 
class  SMatrixTensor
 S matrix for elements in dimensions 2 and 3 with tensorized shape functions. More...
 
class  SolverConjugate
 Solver for a complex system. More...
 
class  SolverFabric
 Abstract fabric class for linear solvers. More...
 
class  SourceFunctionF0_x
 Design of the limit order source function in $x$ direction as $\nabla p_0$. More...
 
class  SourceFunctionF0_y
 Design of the limit order source function in $y$ direction as $\nabla p_0$. More...
 
class  Space
 Abstract class for a space. More...
 
class  SpaceDebug
 Class for output of all elements of a class, good for debugging. More...
 
class  SpaceGraph
 
class  SpaceHelper
 Class which helps to build the T Columns of the elements of a space, with the help of a space pre builder. More...
 
class  SpaceNotBuilt
 Indicates that the space on which a function was called was not yet correctly built. More...
 
class  SpaceOnCells
 Abstract class for a space. More...
 
class  SpaceOnCoarseCells
 Interface class for SpacesOnCells that also allow for allCells(), that i.e. More...
 
class  SpacePreBuilder
 
class  SparseMatrix
 Sparse matrix. More...
 
class  Sphere
 Topological sphere connector. More...
 
class  Sphere3d
 Geometric sphere element. More...
 
struct  SphereMapping
 Geometric sphere. More...
 
class  SphericalFormula
 
class  SphericalFormula< Real >
 Formula in spherical polar coordinates. More...
 
class  SphericalFormula< Real2d >
 Class representing SphericalFormulas in two in 2 components. More...
 
class  SphericalSurface
 Topological spherical surface connector. More...
 
class  SphericalSurface3d
 Geometric spherical surface element. More...
 
class  Spooles
 Sparse direct solver for symmetric and unsymmetric matrices. More...
 
class  Square
 Mesh for $[0,1]^2$ with one quadrilateral. More...
 
class  Square2
 Mesh for $[0,1]^2$ with two quadrilaterals. More...
 
class  Squared
 The square of a element function (componentwise) More...
 
class  SquareOneInfiniteRect
 Mesh consisting of two cells, one Quad2d and one InfiniteRect2d. More...
 
class  SquareTwoInfiniteRects
 Mesh consisting of three cells, one Quad2d and two InfiniteRect2d. More...
 
class  Stacktrace
 Dumps a stack trace using gdb. More...
 
class  StiffArray
 An array of objects of fix length, defined by template parameter dim. More...
 
class  StiffArray< 0, F >
 Stiff Array of zero dimension makes no sense. More...
 
class  StiffArray< 1, F >
 
class  StlVectorScan
 Scanner working on std::vector elements. More...
 
class  StraightPeriodicBoundary
 
class  StrategyChange
 Exception indicating that changing the subdivision strategy is not allowed (but was tried anyway). More...
 
class  Subdivision
 Common base class for QuadSubdivision and HexSubdivision. More...
 
class  SubMatrix
 
class  SubMatrixN
 Abstract class for an operator, which is a sub matrix of another matrix. More...
 
class  Subspace
 Class for holding an offset of global indices of space. More...
 
class  SubspaceHelper
 
class  SubVector
 A sub vector, defined by another vector and an index set. More...
 
class  SuperLU
 Direct sparse solver for unsymmetric matrices. More...
 
class  SuperLUFabric
 Fabric class for SuperLU. More...
 
class  Symmetry
 General class for symmetries on a geometrical object. More...
 
class  Symmetry< Edge >
 Specialized template for edges. More...
 
class  Symmetry< Quad >
 Specialized template for quadrilaterons. More...
 
class  TColumn
 A column of a T matrix. More...
 
class  TColumnBlock
 A column of a T matrix. More...
 
class  TColumnSet
 A set of TColumns and polynomial degrees, sorted by a key, eg. More...
 
class  TColumnTensor
 A column of a T matrix. More...
 
class  TensorVertexMap
 Basic template class for a tensor map vertex. More...
 
class  TensorVertexMap< 1 >
 
class  TensorVertexMap< 2 >
 
class  TensorVertexMap< 3 >
 
class  Tetrahedron
 A tetrahedron in the topology. More...
 
class  Tetrahedron3d
 A 3D cell: tetrahedron. More...
 
class  TIndex
 T matrix for linear and regular elements. More...
 
class  TMatrix
 A T matrix in sparse notation. More...
 
class  TMatrixBase
 An abstract class for a T matrix. More...
 
class  TMatrixBlock
 TMatrixBlock are special Tmatrices in block diagonal structure, builded with two Tmatrices itsself. More...
 
class  Transpose
 The transpose of another matrix. More...
 
class  Triangle
 A triangle in the topology. More...
 
class  Triangle2d
 A 2D cell: triangle. More...
 
class  Triangle3d
 A 3D cell: triangle. More...
 
class  TrivExtendRestrict
 Trivial extension and restriction operator. More...
 
class  Umfpack
 Sparse direct solver for unsymmetric matrices. More...
 
class  UmfpackFabric
 Fabric class for Umfpack. More...
 
class  UniformlyRefinedMesh2
 Wrapper class refining an existing 2d mesh uniformly. More...
 
class  UnitNd
 A vector of dimension dim and length 1. More...
 
class  VecOperator
 Abstract class for an operator acting on vectors only, not arbitrary functions. More...
 
class  Vector
 A vector. More...
 
class  VectorElementFormula
 
class  VectorElementFormula< F, 2, G >
 
class  VectorElementFormula< F, 3, G >
 
class  VectorElementFormulaBase
 Element formula returning a vector. More...
 
class  VectorFormula
 Element formula returning a vector. More...
 
class  Vertex
 A vertex in the topology. More...
 
class  VertexData
 Stores additional information on a vertex, namely its cells and edges. More...
 
class  VertexQuad2d
 A 2D element map for a quadrilateral given by a the four vertices. More...
 
class  VertexTriangle2d
 A 2D element map for a triangle. More...
 
class  WrongInputException
 Exception class to express an input criteria was not met. More...
 
class  WrongRelations
 Exception class to express an illegal relation within topological lists. More...
 
class  Wsym_x
 
class  Wsym_y
 
class  Wunsym_x
 
class  Wunsym_y
 
class  Z2
 Binary group (algebraic): only the values 0 and 1 are represented. More...
 
class  Z3
 Algebraic group with three elements: 0, 1 and 2. More...
 
class  Z4
 Algebraic group with four elements: 0, 1, 2 and 3. More...
 
class  ZylindricalFormula
 Formula in zylindrical coordinates. More...
 

Typedefs

typedef std::complex< Real > Cmplx
 Type for a complex number. It also depends on the setting of Real. More...
 
typedef Point< Cmplx, 1 > Cmplx1d
 
typedef Point< Cmplx, 2 > Cmplx2d
 
typedef Point< Cmplx, 3 > Cmplx3d
 
typedef Mapping< Cmplx, 2 > MapCmplx2d
 
typedef Mapping< Cmplx, 3 > MapCmplx3d
 
typedef Mapping< Real, 2 > MapReal2d
 
typedef Mapping< Real, 3 > MapReal3d
 
typedef double Real
 Type normally used for a floating point number. More...
 
typedef Point< Real, 1 > Real1d
 
typedef Point< Real, 2 > Real2d
 
typedef Point< Real, 3 > Real3d
 
typedef Scan< Cell1 > Scan1
 A scanner for a 1D mesh. More...
 
typedef Scan< Cell2 > Scan2
 A scanner for a 2D mesh. More...
 
typedef Scan< Cell3 > Scan3
 A scanner for a 3D mesh. More...
 
typedef Scan< Connector0 > ScanCntr0
 
typedef Scan< Connector1 > ScanCntr1
 
typedef Scan< Connector2 > ScanCntr2
 
typedef std::set< const std::type_info * > set_info
 
typedef signed int sint
 Abbreviation for signed int. More...
 
typedef unsigned char uchar
 Abbreviation for unsigned char. More...
 
typedef UnitNd< 1 > Unit1d
 
typedef UnitNd< 2 > Unit2d
 
typedef UnitNd< 3 > Unit3d
 
typedef unsigned short ushort
 Abbreviation for unsigned short. More...
 

Enumerations

enum  Basis { Default = 0, BND }
 Enum representing the basis evaluation type of a Linearform ALL - standard linearform evaluation on all basis functions of a element BND - linearform evaluation just on basisfunctions on the boundary, in 1D : nodal in 2D : nodal and edge basis in 3D : nodal, edge, face this applicates for tensored basis functions on hp2D::Quad only at the moment. More...
 
enum  dimproj { dimX, dimY, dimZ, dimdiv }
 
enum  intRule { GAUSS_LOBATTO = 0, GAUSS_JACOBI = 4, TRAPEZE = 5 }
 Types of integration rules to choose from. More...
 
enum  Optimize { MIN, MAX }
 

Functions

template<class F >
void addExactDtN_Circle2D (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff)
 Add DtN contribution for a circular boundary. More...
 
template<class F , class G >
void addExactDtN_Circle2D (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, Vector< Cmplx > &rhs, const ElementFormula< G > &frm, const Sequence< F > DtNCoeffRhs)
 
void addExactDtN_Circle2D (Matrix< Real > &dest, const SpaceOnCells< Real > &spc, const Sequence< Real > DtNCoeff)
 Add DtN contribution for a circular boundary. More...
 
void addExactDtN_Circle2D (Matrix< Real > &dest, const SpaceOnCells< Real > &spc, const Sequence< Real > DtNCoeff, Vector< Real > &rhs, const ElementFormula< Real > &frm, const Sequence< Real > DtNCoeffRhs)
 
template<class F >
void addExactDtN_X_2D (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F , class G >
void addExactDtN_X_2D (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, Vector< Cmplx > &rhs, const ElementFormula< G > &frm, const Sequence< F > DtNCoeffRhs, const Real L=1.0)
 
void addExactDtN_X_2D (Matrix< Real > &dest, const SpaceOnCells< Real > &spc, const Sequence< Real > DtNCoeff, const Real L=1.0)
 
template<class F >
void addExactDtN_X_2Dcos (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F , class G >
void addExactDtN_X_2Dcos (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, Vector< Cmplx > &rhs, const ElementFormula< G > &frm, const Sequence< F > DtNCoeffRhs, const Real L=1.0)
 
template<class F , class G >
void addExactDtN_X_2Dcos_wp (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, Vector< Cmplx > &rhs, const G &frm, const Sequence< F > DtNCoeffRhs, const Real L=1.0)
 
template<class F >
void addExactDtN_X_2Dcossin (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F , class G >
void addExactDtN_X_2Dcossin (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, Vector< Cmplx > &rhs, const ElementFormula< G > &frm, const Sequence< F > DtNCoeffRhs, const Real L=1.0)
 
template<class F , class G >
void addExactDtN_X_2Dcossin_wp (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, Vector< Cmplx > &rhs, const G &frm, const Sequence< F > DtNCoeffRhs, const Real L=1.0)
 
template<class F >
void addExactDtN_X_2Dsin (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F , class G >
void addExactDtN_X_2Dsin (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, Vector< Cmplx > &rhs, const ElementFormula< G > &frm, const Sequence< F > DtNCoeffRhs, const Real L=1.0)
 
template<class F , class G >
void addExactDtN_X_2Dsin_wp (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, Vector< Cmplx > &rhs, const G &frm, const Sequence< F > DtNCoeffRhs, const Real L=1.0)
 
template<class F >
void addExactDtN_X_2Dsincos (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F , class G >
void addExactDtN_X_2Dsincos (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, Vector< Cmplx > &rhs, const ElementFormula< G > &frm, const Sequence< F > DtNCoeffRhs, const Real L=1.0)
 
template<class F , class G >
void addExactDtN_X_2Dsincos_wp (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, Vector< Cmplx > &rhs, const G &frm, const Sequence< F > DtNCoeffRhs, const Real L=1.0)
 
template<class F >
void addExactDtN_X_2Dsym (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F >
void addExactDtN_X_2Dunsym (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F >
void addExactDtN_Y_2D (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F , class G >
void addExactDtN_Y_2D (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, Vector< Cmplx > &rhs, const ElementFormula< G > &frm, const Sequence< F > DtNCoeffRhs, const Real L=1.0)
 
template<class F >
void addExactDtN_Y_2Dcos (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F >
void addExactDtN_Y_2Dcossin (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F >
void addExactDtN_Y_2Dsin (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F >
void addExactDtN_Y_2Dsincos (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F >
void addExactDtN_Y_2Dsym (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F >
void addExactDtN_Y_2Dunsym (Matrix< Cmplx > &dest, const SpaceOnCells< Real > &spc, const Sequence< F > DtNCoeff, const Real L=1.0)
 
template<class F , uint dim>
Mapping< F, dim > adjugate (const Mapping< F, dim > &m)
 
template<class F , uint dim>
Mapping< F, dim > & adjugate (Mapping< F, dim > &m)
 
template<class F , class G >
Sequence< G * > allConnectors (const F &cntr, G *(F::*fun)(uint) const)
 Return all connectors of a particular type of another connector, e.g. More...
 
template<class F , class G >
void allConnectors (const F &cntr, G *(F::*fun)(uint) const, Set< G * > &set)
 Return all connectors of a particular type of another connector, e.g. More...
 
template<class F , class H , class I >
void apply (Operator< F > &op, const Matrix< H > &mX, Matrix< I > &mY)
 Multiplication with a matrix. More...
 
Real besselJ0 (const Real x)
 
Real besselJ1 (const Real x)
 
Real besselJn (const Real x, const int n)
 Evaluates the Bessel function $J_n(x)$. More...
 
Sequence< Real > besselJn (const Real x, const Sequence< int > &n)
 Evaluates the Bessel function $J_n(x)$ for several orders. More...
 
Real besselY0 (const Real x)
 
Real besselY1 (const Real x)
 
Real besselYn (const Real x, const int n)
 Evaluates the Bessel function $ Y_n(x) $. More...
 
void buildEdgeMesh (Scan2 *sc, const concepts::Set< uint > attrib, MutableMeshBase &emsh)
 Construct a mesh of edges of a 2D mesh w.r.t. More...
 
void chebychevPoints (concepts::Array< Real > &p)
 Zeros of Chebychev polynomials in [-1,1]. More...
 
const Cmplx cmplx_i (0, 1)
 
template<class F , uint dim>
Array< F > componentArray (const Array< Point< F, dim >> &a, uint i)
 Returns the component array of an array of vectors. More...
 
const concepts::Array< Real > computeKarniadakisValues (uint np, const Real *absc, uint npx, uint type)
 Evaluate (transformed) Karniadakis Shapefunctions up to a order np on requested abcissa points in [0,1]. More...
 
template<class F >
void convertCCS_rowSorting (F &m, typename F::type *a, int *asub, int *xa)
 Method converts a matrix of type F to Sparse Column Storage (CCS) format. More...
 
template<class F >
void convertCRS_rowSorting (F &m, typename F::value_type *a, int *asub, int *xa)
 Method converts a matrix of type F to Sparse Row Storage (CRS) format. More...
 
template<class F >
void convertIJK_unSorted (F &m, typename F::type *a, int *irn, int *jcn)
 
template<class T >
Teuchos::RCP< Belos::SolverManager< T, Tpetra::MultiVector< T, int >, Tpetra::Operator< T > > > createBelosSolverMgr (std::string solverType, const Teuchos::RCP< Teuchos::ParameterList > &solverParam, Teuchos::RCP< Belos::LinearProblem< T, Tpetra::MultiVector< T, int >, Tpetra::Operator< T > > > linearProblem)
 Sets the solver type to one of the followings. More...
 
template<class T >
Teuchos::RCP< Ifpack2::Preconditioner< T > > createIfpackPrec (std::string precType, Teuchos::RCP< Teuchos::ParameterList > precParam, const Teuchos::RCP< const Tpetra::CrsMatrix< T, int > > A)
 precType can assume the following parameters More...
 
std::string demangle (const char *name)
 Returns the class name of a typeid name return statement. More...
 
template<class F , uint dim>
F determinant (const Mapping< F, dim > &m)
 
std::string ensureEnding (const std::string &filename, const std::string ending)
 Returns a string with particular ending. More...
 
Real3d evaluatepermutation (const Real3d p, const int index)
 Evaluation of a 3d permutation. More...
 
template<class exc >
exc exception_set_fields (exc e, const std::string &file, const unsigned int line, const std::string &function, const std::string &excName)
 Sets fields on exception and throws it. More...
 
template<class exc >
void exception_throw_assert (const std::string &file, int line, const std::string &function, const std::string &exc_name, const std::string &cond, exc e)
 Sets the fields of an assertion and throws it. More...
 
Cmplx g_fast (const Real L, const Real omega, const Real c, const Real rho0, const Real nu, const uint j)
 Compute the coefficients. More...
 
Cmplx g_slow (const Real L, const Real omega, const Real c, const Real rho0, const Real nu, const uint j)
 Compute the coefficients. More...
 
void GaussJacobiAbscWght (double *x, double *w, const uint p)
 Computes and returns the integration weights and abscissas for the Gauss Jacobi integration. More...
 
void GaussLobattoAbscWght (double *x, double *w, const uint p, const uint j=0)
 Computes and returns the integration weights and abscissas for the Gauss (Jacobi) Lobatto integration. More...
 
void GaussRadauAbscWght (double *x, double *w, const uint p, const uint j=0)
 Computes and returns the integration weights and abscissas for the Gauss Radau Jacobi integration. More...
 
template<uint dimC>
void getChild (const typename JacobianCell< dimC >::cell &cCell, const Point< Real, dimC > &eta, const std::array< Real, std::size_t(dimC)> x0, const std::array< Real, std::size_t(dimC)> xN, const typename JacobianCell< dimC >::cell *&cld)
 Searches through the dichotomic tree cell hierachy to find the unique child cell that is defined via the local point eta in [0,1]^dimC. More...
 
std::string getDirectory (const std::string str)
 Returns the directory of a given full filename. More...
 
std::string getFilename (const std::string str)
 Returns the filename (with ending) of a given full filename. More...
 
std::string getFilenamePrefix (const std::string str)
 Returns the prefix of a given full filename, e.g. More...
 
Sequence< Cmplx > getHelmholtzDtNCoeff_Circle2D (const Real omega, const Real R, uint N=0)
 Returns the coefficients for a non-local DtN map for the Helmholtz operator with frequency omega for a circular boundary of radius R which is truncated at order N. More...
 
Sequence< Cmplx > getHelmholtzDtNCoeff_Straight2D (const Real omega, const Real L, uint N=0)
 Returns the coefficients for a non-local DtN map for the Helmholtz operator with frequency omega for a straight boundary of length L which is truncated at order N. More...
 
Sequence< Real > getLaplaceDtNCoeff_Circle2D (const Real R, uint N=0)
 Returns the coefficients for a non-local DtN map for the Laplace operator for a circular boundary of radius R which is truncated at order N. More...
 
Sequence< Real > getLaplaceDtNCoeff_Straight2D (const Real L, uint N=0)
 Returns the coefficients for a non-local DtN map for the Laplace operator for a straight boundary of length L which is truncated at order N. More...
 
Sequence< Cmplx > getNSDtNCoeff_Straight2D_partDn (const Real L, const Real omega, const Real c, const Real rho0, const Real nu, uint N=0)
 
Sequence< Cmplx > getNSDtNCoeff_Straight2D_partDt (const Real L, const Real omega, const Real c, const Real rho0, const Real nu, uint N=1)
 
Sequence< Cmplx > getNSDtNCoeff_Straight2D_partDttilde (const Real L, const Real omega, const Real c, const Real rho0, const Real nu, uint N=1)
 
Sequence< Cmplx > getNSDtNCoeff_Straight2D_partRn (const Real L, const Real omega, const Real c, const Real rho0, const Real nu, uint N=1)
 
Sequence< Cmplx > getNSDtNCoeff_Straight2D_partRntilde (const Real L, const Real omega, const Real c, const Real rho0, const Real nu, uint N=1)
 
Sequence< Cmplx > getNSDtNCoeff_Straight2D_partRt (const Real L, const Real omega, const Real c, const Real rho0, const Real nu, uint N=0)
 
template<class F >
uint getNumberofRows (F &m)
 
template<class F >
uint getNumberofRows (HashedSparseMatrix< F > &m)
 
Cmplx hankel_1_deriv_n (const Real x, const int n)
 Evaluates the derivative $ H^{(1)}_n{}'(x) $ of the Hankel function $ H^{(1)}_n(x) = J_n(x) + \mathrm{i}Y_n(x) $. More...
 
Sequence< Cmplx > hankel_1_deriv_n (const Real x, const Sequence< int > &n)
 
Cmplx hankel_1_n (const Real x, const int n)
 Evaluates the Hankel function $ H^{(1)}_n(x) = J_n(x) + \mathrm{i}Y_n(x) $. More...
 
Sequence< Cmplx > hankel_1_n (const Real x, const Sequence< int > &n)
 
Cmplx hankel_2_deriv_n (const Real x, const int n)
 Evaluates the derivative $ H^{(2)}_n{}'(x) $ of the Hankel function $ H^{(2)}_n(x) = J_n(x) - \mathrm{i}Y_n(x) $. More...
 
Sequence< Cmplx > hankel_2_deriv_n (const Real x, const Sequence< int > &n)
 
Cmplx hankel_2_n (const Real x, const int n)
 Evaluates the Hankel function $ H^{(2)}_n(x) = J_n(x) - \mathrm{i}Y_n(x) $. More...
 
Sequence< Cmplx > hankel_2_n (const Real x, const Sequence< int > &n)
 
Import2dMeshGeneral * import2dMeshGeneralFromInput (const InOutParameters input, bool verbose=false)
 Loads a mesh from a paramater list. More...
 
template<typename G >
Real integrate (const Element< G > &elm)
 Returns the area of the cell belonging to the element elm. More...
 
template<typename F , typename G >
F integrate (const ElementWithCell< G > &elm, const ElementFormula< F, G > &frm, const Real t=0.0, IntegrationCell::intFormType form=IntegrationCell::ZERO)
 Returns the integral of the element formula frm over the cell belonging to the element elm. More...
 
template<class F , class G >
F integrate (const ElementWithCell< G > &elm1, const ElementWithCell< G > &elm2, const ElementFormula< F, G > &frm1, const ElementFormula< F, G > &frm2, const Real t=0, IntegrationCell::intFormType form=IntegrationCell::ZERO)
 Returns the integral over the element elm1 respective elm2 of the product of the ElementFormulas frm1 and frm2. More...
 
template<class F , typename G >
F integrate (const Sequence< ElementWithCell< G > * > &elm_seq, const ElementFormula< F, G > &frm, const Real t=0.0, IntegrationCell::intFormType form=IntegrationCell::ZERO)
 Returns the integral over elements in sequence elm_seq of the formula or element formula frm at time t. More...
 
template<class F , typename G >
F integrate (const SpaceOnCells< G > &spc, const ElementFormula< F, G > &frm, const Real t=0.0, IntegrationCell::intFormType form=IntegrationCell::ZERO)
 Returns the integral over space spc of the formula or element formula frm at time t. More...
 
template<class F , class G >
F integrate (const SpaceOnCells< G > &spc1, const SpaceOnCells< G > &spc2, const ElementFormula< F, G > &frm1, const ElementFormula< F, G > &frm2, const Real t=0, IntegrationCell::intFormType form=IntegrationCell::ZERO)
 Returns the integral over spc1 respective spc2 of the product of the ElementFormulas frm1 and frm2, where frm1 is given on spc1 and frm2 is given on spc2. More...
 
template<class F >
F inverse (const F &f)
 
template<class F , uint dim>
Mapping< F, dim > inverse (const Mapping< F, dim > &m)
 
template<class F >
F & inverse (F &f)
 
template<class F , uint dim>
Mapping< F, dim > & inverse (Mapping< F, dim > &m)
 
bool isParallelRunning ()
 Tests if the instruction MPI::Init() was called. More...
 
Array< Real > jacobianDeterminant (const Hexahedron3d &Hexa, const Array< QuadratureRule1d * > &ArrayQuad1D)
 Computes a multi-dimensional Jacobian determinant tensor. More...
 
Real jacobianDeterminant (const Hexahedron3d &Hexa, const Real3d &xi)
 Computes the Jacobian determinant $J_K = \text{det}(dF_K)$. More...
 
Array< Mapping< Real, 3, 3 > > jacobianTensor (const Hexahedron3d &Hexa, const Array< QuadratureRule1d * > &ArrayQuad1D)
 Computes a multi-dimensional Jacobian tensor. More...
 
Mapping< Real, 3, 3 > jacobianTensor (const Hexahedron3d &Hexa, const Real3d &xi)
 Compute the Jacobian tensor $dF_K$ that goes from a reference element $\xi \in (0,1)^3$ to M(3,3) More...
 
void JacobiDerivatives (const double alf, const double bet, const int maxn, const double *x, const int m, const double *p, double *q)
 Computes the values of the derivatives of the Jacobi polynomials. More...
 
void JacobiPol (const double alf, const double bet, const int maxn, const double *x, const int m, double *p)
 Computes the values of the Jacobi polynomials. More...
 
void JacobiZeros (double *x, int p, double alf, double bet)
 Computes the zeros of the Jacobi polynomials $P_{p}^{(\alpha,\beta)}(x)$. More...
 
template<typename F , typename G >
Real L2product (const ElementWithCell< G > &elm, const ElementFormula< F, G > &u, const ElementFormula< Real > *c=0, const Real t=0.0, IntegrationCell::intFormType form=IntegrationCell::ZERO)
 Returns the L2 product or with c weighted L2 product of an element formula u over the cell belonging to the element elm. More...
 
template<class F , typename G >
Real L2product (const Sequence< ElementWithCell< G > * > &elm_seq, const ElementFormula< F, G > &u, const ElementFormula< Real > *c=0, const Real t=0.0, IntegrationCell::intFormType form=IntegrationCell::ZERO)
 Returns the L2 product or with c weighted L2 product of an element formula u over the cells belonging to the elements in the sequence elm_seq. More...
 
template<class F , typename G >
Real L2product (SpaceOnCells< F > &spc, const G &u, const ElementFormula< Real > *c=0, const Real t=0.0, IntegrationCell::intFormType form=IntegrationCell::ZERO)
 Returns the L2 product or with c weighted L2 product over space spc of the formula or element formula u at time t. More...
 
Cmplx lambda_j_fast (const Real L, const Real omega, const Real c, const Real rho0, const Real nu, const uint j)
 Compute the eigenvalues. More...
 
Cmplx lambda_j_slow (const Real L, const Real omega, const Real c, const Real rho0, const Real nu, const uint j)
 Compute the eigenvalues. More...
 
Cmplx lambda_limit (const Real omega, const Real c0, const int n, const Real L)
 
template<class FunctionT >
std::shared_ptr< const FunctionT > makeAdaptiveQuadrature (const uint nQuadraturePoints, const intRule quadratureType)
 factory function encapsulating the memory manager More...
 
template<class F , class G >
void makeArray (const F &cell, const Array< Real > &p, G(F::*fun)(Real) const, Array< G > &array)
 Creates an array array by applying an function fun of a cell cell for each value p. More...
 
template<class F , class G >
void makeArray (const F &cell, const Array< Real > &pX, const Array< Real > &pY, const Array< Real > &pZ, G(F::*fun)(Real, Real, Real) const, Array< G > &array, bool istensor=true)
 Creates an array array by applying an function fun of a cell cell for each combination of the values pX and pY. More...
 
template<class F , class G >
void makeArray (const F &cell, const Array< Real > &pX, const Array< Real > &pY, G(F::*fun)(Real, Real) const, Array< G > &array, bool istensor=true)
 Creates an array array by applying an function fun of a cell cell for each combination of the values pX and pY. More...
 
template<class F >
Array< F > makeArray (std::initializer_list< F > list)
 Creates an array from a comma separated list of values. More...
 
template<class T >
RCP< const T > makecRCP_weak (T *x)
 
template<class F >
Sequence< F > makeEquidistantSequence (uint n, const F &first, const F &diff)
 
template<class FunctionT >
std::shared_ptr< const FunctionT > makeQuadrature (const uint nQuadraturePoints, const intRule quadratureType)
 factory function encapsulating the memory manager More...
 
Sequence< int > makeRangeSequence (int start, int afterlast)
 Returns the sequence start, start+1,...,afterlast-1. More...
 
Sequence< int > makeRangeSequence (int start, int afterlast, uint dist)
 Returns the sequence start, start+dist,... More...
 
Sequence< int > makeRangeSequence (uint n)
 Returns the sequence 0,1,...,n-1. More...
 
template<class T >
RCP< T > makeRCP (T *x)
 Function to create a RCP which deletes the object when no RCP points on it anymore. More...
 
template<class T >
RCP< T > makeRCP_weak (T *x)
 Function to create a RCP without deleting the object in the destructor. More...
 
template<class F >
Sequence< F > makeSequence (std::initializer_list< F > list)
 Creates an sequence of length
from a comma separated list of values. More...
 
template<class F >
Sequence< F > makeSequence (uint n, const F &first,...)
 Creates an sequence of length
from a comma separated list of values. More...
 
template<class F >
Set< F > makeSet (std::initializer_list< F > list)
 Creates an array from a comma separated list of values. More...
 
template<class F >
Set< F > makeSet (uint n, const F &first,...)
 Creates an array of length
from a comma separated list of values. More...
 
template<class FunctionT >
std::shared_ptr< const FunctionT > makeShapeFunction (const concepts::QuadratureRule1d &quadratureRule, const uint polynomialDegree)
 factory function encapsulating the memory manager More...
 
int match (const Connector1 &edg0, const Connector1 &edg1, int idx[])
 Checks, if two edges has a common vertex. More...
 
template<class F , class G , class H >
void matrixMultiplyRowSorting (const F &factL, const G &factR, Matrix< H > &dest)
 Multiplies two matrices, which deliver at least a row sorted iterator, and adds (!) the result to a third matrix. More...
 
template<typename F , typename G >
void memorycpy (F *dest, const G *src, size_t n)
 Copies n entries from src to dest (faster than std::memcpy) More...
 
template<class F >
F * newField (uint nr)
 Reserve memory for a field of type F and returns the pointer to first entrance. More...
 
template<class _Tp , class _Ref , class _Ptr >
bool operator!= (const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &__x, const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &__y)
 
template<class _Tp , class _RefL , class _PtrL , class _RefR , class _PtrR >
bool operator!= (const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &__x, const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &__y)
 
BilinearFormContainer< Cmplx > operator* (const BilinearFormContainer< Cmplx > frm1, const Cmplx w)
 
BilinearFormContainer< Cmplx > operator* (const BilinearFormContainer< Cmplx > frm1, const Real w)
 
BilinearFormContainer< Cmplx > operator* (const BilinearFormContainer< Real > frm1, const Cmplx w)
 
BilinearFormContainer< Real > operator* (const BilinearFormContainer< Real > frm1, const Real w)
 Simple multiplication from right. More...
 
ElementFormulaContainer< MapCmplx2d > operator* (const Cmplx a, const ElementFormulaContainer< MapCmplx2d > frm)
 
ElementFormulaContainer< MapCmplx2d > operator* (const Cmplx a, const ElementFormulaContainer< MapReal2d > frm)
 
BilinearFormContainer< Cmplx > operator* (const Cmplx w, const BilinearFormContainer< Cmplx > frm1)
 
BilinearFormContainer< Cmplx > operator* (const Cmplx w, const BilinearFormContainer< Real > frm1)
 
template<class F , uint dim>
Point< typename Combtype< F, Cmplx >::type, dim > operator* (const Cmplx x, const Point< F, dim > &y)
 
template<class F , class G >
concepts::Array< typename Combtype< F, G >::type > operator* (const concepts::Array< F > &array, const G &val)
 Multiplication operator. More...
 
ElementFormulaContainer< Cmplx > operator* (const ElementFormulaContainer< Cmplx > frm, const Cmplx a)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< Cmplx > frm, const Cmplx2d a)
 
ElementFormulaContainer< Cmplx > operator* (const ElementFormulaContainer< Cmplx > frm, const Real a)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< Cmplx > frm, const Real2d a)
 
ElementFormulaContainer< Cmplx > operator* (const ElementFormulaContainer< Cmplx > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< Cmplx > frm1, const ElementFormulaContainer< Cmplx2d > frm2)
 
ElementFormulaContainer< MapCmplx2d > operator* (const ElementFormulaContainer< Cmplx > frm1, const ElementFormulaContainer< MapCmplx2d > frm2)
 
ElementFormulaContainer< MapCmplx2d > operator* (const ElementFormulaContainer< Cmplx > frm1, const ElementFormulaContainer< MapReal2d > frm2)
 
ElementFormulaContainer< Cmplx > operator* (const ElementFormulaContainer< Cmplx > frm1, const ElementFormulaContainer< Real > frm2)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< Cmplx > frm1, const ElementFormulaContainer< Real2d > frm2)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< Cmplx2d > frm, const Cmplx a)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< Cmplx2d > frm, const Real a)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< Cmplx2d > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Cmplx > operator* (const ElementFormulaContainer< Cmplx2d > frm1, const ElementFormulaContainer< Cmplx2d > frm2)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< Cmplx2d > frm1, const ElementFormulaContainer< Real > frm2)
 
ElementFormulaContainer< Cmplx > operator* (const ElementFormulaContainer< Cmplx2d > frm1, const ElementFormulaContainer< Real2d > frm2)
 
ElementFormulaContainer< MapCmplx2d > operator* (const ElementFormulaContainer< MapCmplx2d > frm, const Cmplx a)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< MapCmplx2d > frm, const Cmplx2d a)
 
ElementFormulaContainer< MapCmplx2d > operator* (const ElementFormulaContainer< MapCmplx2d > frm, const Real a)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< MapCmplx2d > frm, const Real2d a)
 
ElementFormulaContainer< MapCmplx2d > operator* (const ElementFormulaContainer< MapCmplx2d > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< MapCmplx2d > frm1, const ElementFormulaContainer< Cmplx2d > frm2)
 
ElementFormulaContainer< MapCmplx2d > operator* (const ElementFormulaContainer< MapCmplx2d > frm1, const ElementFormulaContainer< Real > frm2)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< MapCmplx2d > frm1, const ElementFormulaContainer< Real2d > frm2)
 
ElementFormulaContainer< MapCmplx2d > operator* (const ElementFormulaContainer< MapReal2d > frm, const Cmplx a)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< MapReal2d > frm, const Cmplx2d a)
 
ElementFormulaContainer< MapReal2d > operator* (const ElementFormulaContainer< MapReal2d > frm, const Real a)
 
ElementFormulaContainer< Real2d > operator* (const ElementFormulaContainer< MapReal2d > frm, const Real2d a)
 
ElementFormulaContainer< MapCmplx2d > operator* (const ElementFormulaContainer< MapReal2d > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< MapReal2d > frm1, const ElementFormulaContainer< Cmplx2d > frm2)
 
ElementFormulaContainer< MapReal2d > operator* (const ElementFormulaContainer< MapReal2d > frm1, const ElementFormulaContainer< Real > frm2)
 
ElementFormulaContainer< Real2d > operator* (const ElementFormulaContainer< MapReal2d > frm1, const ElementFormulaContainer< Real2d > frm2)
 
ElementFormulaContainer< Cmplx > operator* (const ElementFormulaContainer< Real > frm, const Cmplx a)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< Real > frm, const Cmplx2d a)
 
ElementFormulaContainer< Real > operator* (const ElementFormulaContainer< Real > frm, const Real a)
 Simple multiplying of a element formulas by a constant via *-operator. More...
 
ElementFormulaContainer< Real2d > operator* (const ElementFormulaContainer< Real > frm, const Real2d a)
 
ElementFormulaContainer< Cmplx > operator* (const ElementFormulaContainer< Real > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< Real > frm1, const ElementFormulaContainer< Cmplx2d > frm2)
 
ElementFormulaContainer< MapCmplx2d > operator* (const ElementFormulaContainer< Real > frm1, const ElementFormulaContainer< MapCmplx2d > frm2)
 
ElementFormulaContainer< MapReal2d > operator* (const ElementFormulaContainer< Real > frm1, const ElementFormulaContainer< MapReal2d > frm2)
 
ElementFormulaContainer< Real > operator* (const ElementFormulaContainer< Real > frm1, const ElementFormulaContainer< Real > frm2)
 Simple multiplying of two element formulas by *-operator. More...
 
ElementFormulaContainer< Real2d > operator* (const ElementFormulaContainer< Real > frm1, const ElementFormulaContainer< Real2d > frm2)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< Real2d > frm, const Cmplx a)
 
ElementFormulaContainer< Real2d > operator* (const ElementFormulaContainer< Real2d > frm, const Real a)
 
ElementFormulaContainer< Cmplx2d > operator* (const ElementFormulaContainer< Real2d > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Cmplx > operator* (const ElementFormulaContainer< Real2d > frm1, const ElementFormulaContainer< Cmplx2d > frm2)
 
ElementFormulaContainer< Real2d > operator* (const ElementFormulaContainer< Real2d > frm1, const ElementFormulaContainer< Real > frm2)
 
ElementFormulaContainer< Real > operator* (const ElementFormulaContainer< Real2d > frm1, const ElementFormulaContainer< Real2d > frm2)
 
Frm_Product< Cmplx > operator* (const Formula< Cmplx > &frm, const Cmplx a)
 
Frm_Product< Cmplx, Cmplx, Real > operator* (const Formula< Cmplx > &frm, const Real a)
 
Frm_Product< Cmplx > operator* (const Formula< Cmplx > &frm1, const Formula< Cmplx > &frm2)
 
Frm_Product< Cmplx, Cmplx, Real > operator* (const Formula< Cmplx > &frm1, const Formula< Real > &frm2)
 
Frm_Product< Cmplx, Real > operator* (const Formula< Real > &frm, const Cmplx a)
 
Frm_Product< Real > operator* (const Formula< Real > &frm, const Real a)
 
Frm_Product< Cmplx, Real > operator* (const Formula< Real > &frm1, const Formula< Cmplx > &frm2)
 
Frm_Product< Real > operator* (const Formula< Real > &frm1, const Formula< Real > &frm2)
 
template<class F , class G >
Array< typename Combtype< F, G >::type > operator* (const G &val, const Array< F > &array)
 Multiplication operator. More...
 
template<uint dim>
Cmplx operator* (const Point< Cmplx, dim > &a, const Point< Real, dim > &b)
 
template<uint dim>
Cmplx operator* (const Point< Real, dim > &a, const Point< Cmplx, dim > &b)
 
ElementFormulaContainer< MapCmplx2d > operator* (const Real a, const ElementFormulaContainer< MapCmplx2d > frm)
 
ElementFormulaContainer< MapReal2d > operator* (const Real a, const ElementFormulaContainer< MapReal2d > frm)
 
BilinearFormContainer< Cmplx > operator* (const Real w, const BilinearFormContainer< Cmplx > frm1)
 
BilinearFormContainer< Real > operator* (const Real w, const BilinearFormContainer< Real > frm1)
 
template<class F , uint dim>
Point< typename Combtype< F, Real >::type, dim > operator* (const Real x, const Point< F, dim > &y)
 
template<class F , class G >
Sequence< typename Combtype< F, G >::type > operator* (const Sequence< F > seq1, const G factor)
 
template<class F , class G >
Sequence< typename Combtype< F, G >::type > operator* (const Sequence< F > seq1, const Sequence< G > seq2)
 
BilinearFormContainer< Cmplx > operator+ (const BilinearFormContainer< Cmplx > frm1, const BilinearFormContainer< Cmplx > frm2)
 
BilinearFormContainer< Cmplx > operator+ (const BilinearFormContainer< Cmplx > frm1, const BilinearFormContainer< Real > frm2)
 
BilinearFormContainer< Cmplx > operator+ (const BilinearFormContainer< Real > frm1, const BilinearFormContainer< Cmplx > frm2)
 
BilinearFormContainer< Real > operator+ (const BilinearFormContainer< Real > frm1, const BilinearFormContainer< Real > frm2)
 Simple adding two element formulas by +-operator. More...
 
ElementFormulaContainer< Cmplx > operator+ (const ElementFormulaContainer< Cmplx > frm, const Cmplx a)
 
ElementFormulaContainer< Cmplx > operator+ (const ElementFormulaContainer< Cmplx > frm, const Real a)
 
ElementFormulaContainer< Cmplx > operator+ (const ElementFormulaContainer< Cmplx > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Cmplx > operator+ (const ElementFormulaContainer< Cmplx > frm1, const ElementFormulaContainer< Real > frm2)
 
ElementFormulaContainer< Cmplx2d > operator+ (const ElementFormulaContainer< Cmplx2d > frm, const Cmplx2d a)
 
ElementFormulaContainer< Cmplx2d > operator+ (const ElementFormulaContainer< Cmplx2d > frm, const Real2d a)
 
ElementFormulaContainer< Cmplx2d > operator+ (const ElementFormulaContainer< Cmplx2d > frm1, const ElementFormulaContainer< Cmplx2d > frm2)
 
ElementFormulaContainer< Cmplx2d > operator+ (const ElementFormulaContainer< Cmplx2d > frm1, const ElementFormulaContainer< Real2d > frm2)
 
ElementFormulaContainer< Cmplx > operator+ (const ElementFormulaContainer< Real > frm, const Cmplx a)
 
ElementFormulaContainer< Real > operator+ (const ElementFormulaContainer< Real > frm, const Real a)
 Simple adding of a element formulas and a constant via +-operator. More...
 
ElementFormulaContainer< Cmplx > operator+ (const ElementFormulaContainer< Real > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Real > operator+ (const ElementFormulaContainer< Real > frm1, const ElementFormulaContainer< Real > frm2)
 Simple adding two element formulas by +-operator. More...
 
ElementFormulaContainer< Cmplx2d > operator+ (const ElementFormulaContainer< Real2d > frm, const Cmplx2d a)
 
ElementFormulaContainer< Real2d > operator+ (const ElementFormulaContainer< Real2d > frm, const Real2d a)
 
ElementFormulaContainer< Cmplx2d > operator+ (const ElementFormulaContainer< Real2d > frm1, const ElementFormulaContainer< Cmplx2d > frm2)
 
ElementFormulaContainer< Real2d > operator+ (const ElementFormulaContainer< Real2d > frm1, const ElementFormulaContainer< Real2d > frm2)
 
Frm_Sum< Cmplx > operator+ (const Formula< Cmplx > &frm, const Cmplx a)
 
Frm_Sum< Cmplx, Cmplx, Real > operator+ (const Formula< Cmplx > &frm, const Real a)
 
Frm_Sum< Cmplx > operator+ (const Formula< Cmplx > &frm1, const Formula< Cmplx > &frm2)
 
Frm_Sum< Cmplx, Cmplx, Real > operator+ (const Formula< Cmplx > &frm1, const Formula< Real > &frm2)
 
Frm_Sum< Cmplx, Real > operator+ (const Formula< Real > &frm, const Cmplx a)
 
Frm_Sum< Real > operator+ (const Formula< Real > &frm, const Real a)
 Simple adding two formulas by +-operator. More...
 
Frm_Sum< Cmplx, Real > operator+ (const Formula< Real > &frm1, const Formula< Cmplx > &frm2)
 
Frm_Sum< Real > operator+ (const Formula< Real > &frm1, const Formula< Real > &frm2)
 
template<class _Tp , class _Ref , class _Ptr >
_Matrix_iterator_base< _Tp, _Ref, _Ptr > operator+ (ptrdiff_t __n, const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &__x)
 
template<typename _Tp , typename _RefL , typename _PtrL , typename _RefR , typename _PtrR >
_Matrix_iterator_base< _Tp, _RefL, _PtrL >::difference_type operator- (const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &__x, const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &__y)
 
BilinearFormContainer< Cmplx > operator- (const BilinearFormContainer< Cmplx > frm1, const BilinearFormContainer< Cmplx > frm2)
 
BilinearFormContainer< Cmplx > operator- (const BilinearFormContainer< Cmplx > frm1, const BilinearFormContainer< Real > frm2)
 
BilinearFormContainer< Cmplx > operator- (const BilinearFormContainer< Real > frm1, const BilinearFormContainer< Cmplx > frm2)
 
BilinearFormContainer< Real > operator- (const BilinearFormContainer< Real > frm1, const BilinearFormContainer< Real > frm2)
 Simple adding two element formulas by +-operator. More...
 
ElementFormulaContainer< Cmplx > operator- (const ElementFormulaContainer< Cmplx > frm, const Cmplx a)
 
ElementFormulaContainer< Cmplx > operator- (const ElementFormulaContainer< Cmplx > frm, const Real a)
 
ElementFormulaContainer< Cmplx > operator- (const ElementFormulaContainer< Cmplx > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Cmplx > operator- (const ElementFormulaContainer< Cmplx > frm1, const ElementFormulaContainer< Real > frm2)
 
ElementFormulaContainer< Cmplx2d > operator- (const ElementFormulaContainer< Cmplx2d > frm, const Cmplx2d a)
 
ElementFormulaContainer< Cmplx2d > operator- (const ElementFormulaContainer< Cmplx2d > frm, const Real2d a)
 
ElementFormulaContainer< Cmplx2d > operator- (const ElementFormulaContainer< Cmplx2d > frm1, const ElementFormulaContainer< Cmplx2d > frm2)
 
ElementFormulaContainer< Cmplx2d > operator- (const ElementFormulaContainer< Cmplx2d > frm1, const ElementFormulaContainer< Real2d > frm2)
 
ElementFormulaContainer< Cmplx > operator- (const ElementFormulaContainer< Real > frm, const Cmplx a)
 
ElementFormulaContainer< Real > operator- (const ElementFormulaContainer< Real > frm, const Real a)
 Simple subtracting of a element formulas and a constant via –operator. More...
 
ElementFormulaContainer< Cmplx > operator- (const ElementFormulaContainer< Real > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Real > operator- (const ElementFormulaContainer< Real > frm1, const ElementFormulaContainer< Real > frm2)
 Simple subtracting two element formulas by "-"-operator. More...
 
ElementFormulaContainer< Cmplx2d > operator- (const ElementFormulaContainer< Real2d > frm, const Cmplx2d a)
 
ElementFormulaContainer< Real2d > operator- (const ElementFormulaContainer< Real2d > frm, const Real2d a)
 
ElementFormulaContainer< Cmplx2d > operator- (const ElementFormulaContainer< Real2d > frm1, const ElementFormulaContainer< Cmplx2d > frm2)
 
ElementFormulaContainer< Real2d > operator- (const ElementFormulaContainer< Real2d > frm1, const ElementFormulaContainer< Real2d > frm2)
 
ElementFormulaContainer< Cmplx > operator/ (const ElementFormulaContainer< Cmplx > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Cmplx > operator/ (const ElementFormulaContainer< Cmplx > frm1, const ElementFormulaContainer< Real > frm2)
 
ElementFormulaContainer< Cmplx2d > operator/ (const ElementFormulaContainer< Cmplx2d > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Cmplx2d > operator/ (const ElementFormulaContainer< Cmplx2d > frm1, const ElementFormulaContainer< Real > frm2)
 
ElementFormulaContainer< Cmplx > operator/ (const ElementFormulaContainer< Real > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Real > operator/ (const ElementFormulaContainer< Real > frm1, const ElementFormulaContainer< Real > frm2)
 Division of a element formulas by a scalar element formula via /-operator. More...
 
ElementFormulaContainer< Cmplx2d > operator/ (const ElementFormulaContainer< Real2d > frm1, const ElementFormulaContainer< Cmplx > frm2)
 
ElementFormulaContainer< Real2d > operator/ (const ElementFormulaContainer< Real2d > frm1, const ElementFormulaContainer< Real > frm2)
 Division of a vector valued element formulas by a scalar element formula via /-operator. More...
 
template<class F , class G >
Sequence< typename Combtype< F, G >::type > operator/ (const Sequence< F > seq1, const G divisor)
 
template<class F , class G >
Sequence< typename Combtype< F, G >::type > operator/ (const Sequence< F > seq1, const Sequence< G > seq2)
 
template<class _Tp , class _Ref , class _Ptr >
bool operator< (const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &__x, const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &__y)
 
template<class _Tp , class _RefL , class _PtrL , class _RefR , class _PtrR >
bool operator< (const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &__x, const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &__y)
 
bool operator< (const Cell &cell_x, const Cell &cell_y)
 <-operator could be useful for sorting, e.g. in std::set. More...
 
bool operator< (const Connector &cntr_x, const Connector &cntr_y)
 <-operator sorted by the key, it could be useful for sorting, e.g. More...
 
template<class F >
::std::ostream & operator<< (::std::ostream &os, TColumn< F > *T)
 output-operator for pointer to TColumn, gives either 0 or TColumn itself More...
 
template<uint levelDim>
std::ostream & operator<< (std::ostream &os, const AdaptiveAdjust< levelDim > &a)
 
template<int dim>
std::ostream & operator<< (std::ostream &os, const AdaptiveAdjustP< dim > &a)
 
template<class F >
std::ostream & operator<< (std::ostream &os, const AdaptiveControl< F > &c)
 
template<int dim, class F >
std::ostream & operator<< (std::ostream &os, const AdaptiveControlP< dim, F > &a)
 
std::ostream & operator<< (std::ostream &os, const AdaptiveControlTag &c)
 
template<class F >
std::ostream & operator<< (std::ostream &os, const Array< F > &o)
 
std::ostream & operator<< (std::ostream &os, const CellData &c)
 
template<class F >
std::ostream & operator<< (std::ostream &os, const ElementMatrix< F > &o)
 
template<class F >
std::ostream & operator<< (std::ostream &os, const Graph< F > &Value)
 
template<class F >
std::ostream & operator<< (std::ostream &os, const GraphVertex< F > &Value)
 
template<typename T >
std::ostream & operator<< (std::ostream &os, const HashedSparseMatrix< T > &o)
 
std::ostream & operator<< (std::ostream &os, const IndexRange &i)
 
template<class T , unsigned nlnk>
std::ostream & operator<< (std::ostream &os, const Joiner< T, nlnk > &j)
 
template<uint dim>
std::ostream & operator<< (std::ostream &os, const Level< dim > &c)
 
template<class F , uint DimY, uint DimX>
std::ostream & operator<< (std::ostream &os, const Mapping< F, DimY, DimX > &m)
 
template<int number>
std::ostream & operator<< (std::ostream &os, const Orders< number > &o)
 
template<class F , uint dim>
std::ostream & operator<< (std::ostream &os, const Point< F, dim > &p)
 
std::ostream & operator<< (std::ostream &os, const Quad2d::Index &i)
 
template<class F , class G >
std::ostream & operator<< (std::ostream &os, const std::map< F, G * > &m)
 
template<class F , class G >
std::ostream & operator<< (std::ostream &os, const std::map< F, G > &m)
 
std::ostream & operator<< (std::ostream &os, const std::map< uint, IndexRange > &map)
 
template<class F , class G >
std::ostream & operator<< (std::ostream &os, const std::pair< F, G > &p)
 
template<class F >
std::ostream & operator<< (std::ostream &os, const std::unique_ptr< F > &p)
 
template<class T >
std::ostream & operator<< (std::ostream &os, const std::vector< T * > &field)
 
std::ostream & operator<< (std::ostream &os, const Triangle2d::Index &i)
 
std::ostream & operator<< (std::ostream &os, const Triangle3d::Index &i)
 
template<class F >
std::ostream & operator<< (std::ostream &os, std::unique_ptr< F > &a)
 Output operator for unique_ptr's. More...
 
template<class _Tp , class _Ref , class _Ptr >
bool operator<= (const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &__x, const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &__y)
 
template<class _Tp , class _RefL , class _PtrL , class _RefR , class _PtrR >
bool operator<= (const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &__x, const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &__y)
 
template<class _Tp , class _Ref , class _Ptr >
bool operator== (const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &__x, const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &__y)
 
template<class _Tp , class _RefL , class _PtrL , class _RefR , class _PtrR >
bool operator== (const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &__x, const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &__y)
 
template<class F >
bool operator== (const Array< F > &x, const Array< F > &y)
 
template<class F >
bool operator== (const Array< F > &x, F &y)
 
template<class F , uint dim>
bool operator== (const Point< F, dim > &x, const Point< F, dim > &y)
 
template<class F >
bool operator== (F &y, const Array< F > &x)
 
template<class _Tp , class _Ref , class _Ptr >
bool operator> (const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &__x, const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &__y)
 
template<class _Tp , class _RefL , class _PtrL , class _RefR , class _PtrR >
bool operator> (const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &__x, const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &__y)
 
template<class _Tp , class _Ref , class _Ptr >
bool operator>= (const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &__x, const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &__y)
 
template<class _Tp , class _RefL , class _PtrL , class _RefR , class _PtrR >
bool operator>= (const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &__x, const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &__y)
 
template<class F >
std::istream & operator>> (std::istream &is, BaseSequence< F > &seq)
 
template<class F >
std::istream & operator>> (std::istream &is, BaseSet< F > &set)
 
template<class F >
std::ostream & outputMatlab (std::ostream &os, const ElementMatrix< F > &em)
 Function for output of ElementMatrix to Matlab. More...
 
template<typename T >
std::ostream & outputMatlab (std::ostream &os, const std::complex< T > &val)
 
template<typename T >
std::ostream & outputMatlab (std::ostream &os, const T &val)
 Function for output of basic types to matlab. More...
 
std::ostream & outputMatlab (std::ostream &os, const TMatrix< Real > &T)
 Function for output of T-Matrix to Matlab. More...
 
std::ostream & outputMatlab (std::ostream &os, const TMatrixBase< Real > &T)
 Function for output of T-Matrix base class to Matlab. More...
 
template<class F >
void pointerOutput (std::ostream &os, const Array< F > &array)
 
template<class F >
void pointerOutput (std::ostream &os, const F &val)
 
template<class F >
void pointerOutput (std::ostream &os, const F *val)
 
template<class F >
void pointerOutput (std::ostream &os, F *val)
 
template<class F , uint dim>
Mapping< F, dim > prodTranspose (const Mapping< F, dim > &m)
 
template<class F , uint dim>
Mapping< F, dim > & prodTranspose (Mapping< F, dim > &m)
 
template<class F , class G >
G product (const F &m, const G &v)
 
template<class F , class G >
G & product (const F &m, G &v)
 
Array< Real > quadratureWeightTensor (const Array< QuadratureRule1d * > &ArrayQuad1D)
 Computes a multi-dimensional quadrature weight tensor. More...
 
Real quadratureWeightTensor (const Array< QuadratureRule1d * > &ArrayQuad1D, const Array< int > &Index)
 Compute a quadrature weight tensor at a partical index point. More...
 
concepts::Sequence< Cmplx > ReadEigenValuesFromFile (const int NDtN_given, const std::string Filename)
 
Sequence< Real > realSeqFromStringWithPower (const std::string s)
 Converts a string to a sequence of real numbers, where a power may be allowed to express, e.g., negative powers of 2. More...
 
std::string removeAllWhite (const std::string str)
 Removes all white space in the string str. More...
 
template<class F , class G >
F * securePointer (const F value, const G *matrix)
 
template<class F , class G >
F * securePointer (F &value, G *matrix)
 Templated function, which prevent a pointer to a temporary value got from constant matrices with index operator . More...
 
int sgn (const Real d)
 
template<typename F >
void sparseLineToArrays (std::map< int, F > &line, F *a, int *asub)
 This function converts a sparse line to an array of values and an array of indices. More...
 
std::vector< std::string > splitString (const std::string text, const std::string separators)
 Split the string text string into words, where the separation token are included in separators. More...
 
std::vector< std::string > splitStringByComma (const std::string text)
 Split a strings in words separated by commas while respecting the bracket hierachies. More...
 
std::vector< std::string > splitStringNameParams (const std::string text)
 Split a string like "Ellipse(1.0, 4)" into "Ellipse", "1.0", "4". More...
 
Real sqr (const Real x)
 
template<class F >
bool storeDenseMatrixToMatlab (F &matrix, const uint nofRows, const uint nofCols, const std::string filename, std::string name="", bool append=false)
 Stores a matrix to the matlab file filename as dense matrix name. More...
 
template<class F >
void storeDenseMatrixToMatlab (F &matrix, const uint nofRows, const uint nofCols, std::ostream &ofs, std::string name="")
 Writes a matrix to the stream ofs as dense matrix name in Matlab format. More...
 
template<class F >
void storeSparseMatrixToOctave (SparseMatrix< F > &matrix, std::ostream &ofs, std::string name="")
 Writes a matrix to the stream ofs as dense matrix name in Octave format (older version don't have sparse matrix format). More...
 
template<class F >
std::string stringSubs (const std::string str, const std::string var, F value)
 Substitute all occurances of a substring var of a string str by value which may be for example a real or another string. More...
 
std::string stringtolower (const std::string s)
 
char tolower (const char ch)
 
template<class F , uint dim>
Mapping< F, dim > transpose (const Mapping< F, dim > &m)
 
template<class F , uint dim>
Mapping< F, dim > & transpose (Mapping< F, dim > &m)
 
template<class T >
std::string typeOf (const T &t)
 Return the typeid name of a class object. More...
 
Sequence< concepts::Set< uint > > uintSeqSets (const std::string s)
 Converts a string to a sequence of sets of uint. More...
 
Cmplx visc_ell_fast (const Cmplx lambda, const Real nu, const Real omega, const Real rho0)
 
Cmplx visc_ell_slow (const Cmplx lambda, const Real nu, const Real omega, const Real rho0, const Real c0)
 

Variables

static uint storeDenseMatrixMatlabCounter_ = 0
 Counts number of Matlab outputs (used to uniquely name the matrices) More...
 
static uint storeSparseMatrixMatlabCounter_ = 0
 

Detailed Description

Basic namespace for Concepts-2.

Waveprop.

@toolbox/resultsTable.hh

file geometry/connectorSequence.hh

file geometry/cellConditions.hh

Additional modules may be placed in a different namespace (or one which is nested into this one).

Boundary conditions

Sets for Connectors.

Todo:
replace explicit occurrences of Pi by a namespace constant
Author
Holger Brandsmeier, ETHZ, 2011
Christian Heier, TUB, 2012

write table of results

Classes for physical sources and formulas for both Cartisian and Radial PML

Typedef Documentation

◆ Cmplx

typedef std::complex<Real> concepts::Cmplx

Type for a complex number. It also depends on the setting of Real.

Examples
arpackppTutorial.cc, BGT_0.cc, exactDtN.cc, and matfileTutorial.cc.

Definition at line 39 of file typedefs.hh.

◆ Cmplx1d

typedef Point<Cmplx, 1> concepts::Cmplx1d

Definition at line 20 of file vectorsMatricesForward.hh.

◆ Cmplx2d

typedef Point<Cmplx, 2> concepts::Cmplx2d

Definition at line 21 of file vectorsMatricesForward.hh.

◆ Cmplx3d

typedef Point<Cmplx, 3> concepts::Cmplx3d

Definition at line 22 of file vectorsMatricesForward.hh.

◆ MapCmplx2d

typedef Mapping<Cmplx, 2> concepts::MapCmplx2d

Definition at line 627 of file vectorsMatrices.hh.

◆ MapCmplx3d

typedef Mapping<Cmplx, 3> concepts::MapCmplx3d

Definition at line 628 of file vectorsMatrices.hh.

◆ MapReal2d

typedef Mapping<Real, 2> concepts::MapReal2d

Definition at line 625 of file vectorsMatrices.hh.

◆ MapReal3d

typedef Mapping<Real, 3> concepts::MapReal3d

Definition at line 626 of file vectorsMatrices.hh.

◆ Real

typedef double concepts::Real

Type normally used for a floating point number.

The idea behind this: if you want to have single or quadruple precision instead of double precision, just change this typdef and recompile.

Examples
BGT_0.cc, exactDtN.cc, howToGetStarted.cc, hpFEM2d-simple.cc, hpFEM2d.cc, hpFEM3d-EV.cc, inhomDirichletBCs.cc, inhomDirichletBCs.py, inhomDirichletBCsLagrange.cc, inhomNeumannBCs.cc, linearDG1d.cc, linearFEM1d-simple.cc, linearFEM1d.cc, matfileTutorial.cc, meshes.cc, parallelizationTutorial.cc, and RobinBCs.cc.

Definition at line 36 of file typedefs.hh.

◆ Real1d

typedef Point<Real, 1> concepts::Real1d

Definition at line 17 of file vectorsMatricesForward.hh.

◆ Real2d

typedef Point<Real, 2> concepts::Real2d

Definition at line 18 of file vectorsMatricesForward.hh.

◆ Real3d

typedef Point<Real, 3> concepts::Real3d

Definition at line 19 of file vectorsMatricesForward.hh.

◆ Scan1

typedef Scan<Cell1> concepts::Scan1

A scanner for a 1D mesh.

Definition at line 59 of file mesh.hh.

◆ Scan2

typedef Scan<Cell2> concepts::Scan2

A scanner for a 2D mesh.

Definition at line 62 of file mesh.hh.

◆ Scan3

typedef Scan<Cell3> concepts::Scan3

A scanner for a 3D mesh.

Definition at line 65 of file mesh.hh.

◆ ScanCntr0

typedef Scan<Connector0> concepts::ScanCntr0

Definition at line 51 of file mesh_p.hh.

◆ ScanCntr1

typedef Scan<Connector1> concepts::ScanCntr1

Definition at line 52 of file mesh_p.hh.

◆ ScanCntr2

typedef Scan<Connector2> concepts::ScanCntr2

Definition at line 53 of file mesh_p.hh.

◆ set_info

typedef std::set<const std::type_info*> concepts::set_info

Definition at line 23 of file matfileIO.hh.

◆ sint

typedef signed int concepts::sint

Abbreviation for signed int.

Definition at line 42 of file typedefs.hh.

◆ uchar

typedef unsigned char concepts::uchar

Abbreviation for unsigned char.

Definition at line 45 of file typedefs.hh.

◆ Unit1d

typedef UnitNd<1> concepts::Unit1d

Definition at line 27 of file vectorsMatricesForward.hh.

◆ Unit2d

typedef UnitNd<2> concepts::Unit2d

Definition at line 28 of file vectorsMatricesForward.hh.

◆ Unit3d

typedef UnitNd<3> concepts::Unit3d

Definition at line 29 of file vectorsMatricesForward.hh.

◆ ushort

typedef unsigned short concepts::ushort

Abbreviation for unsigned short.

Definition at line 48 of file typedefs.hh.

Enumeration Type Documentation

◆ Basis

enum concepts::Basis

Enum representing the basis evaluation type of a Linearform ALL - standard linearform evaluation on all basis functions of a element BND - linearform evaluation just on basisfunctions on the boundary, in 1D : nodal in 2D : nodal and edge basis in 3D : nodal, edge, face this applicates for tensored basis functions on hp2D::Quad only at the moment.

Note that in the BND case for tensored quad the Elementmatrix have different size, i.e. em.size = 2 in 1D, em.size = 2*(elm.px + elm.py) in 2D, ... The order stays first x then y.

Further possible types : INNER, etc..

Enumerator
Default 
BND 

Definition at line 55 of file linearForm.hh.

◆ dimproj

enum concepts::dimproj
Enumerator
dimX 
dimY 
dimZ 
dimdiv 

Definition at line 32 of file DtNmap2D_visc.hh.

◆ intRule

enum concepts::intRule

Types of integration rules to choose from.

Enumerator
GAUSS_LOBATTO 
GAUSS_JACOBI 
TRAPEZE 

Definition at line 13 of file defines.hh.

◆ Optimize

enum concepts::Optimize
Enumerator
MIN 
MAX 

Definition at line 26 of file extrema.hh.

Function Documentation

◆ addExactDtN_Circle2D() [1/4]

template<class F >
void concepts::addExactDtN_Circle2D ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff 
)

Add DtN contribution for a circular boundary.

Parameters
destMatrix for the problem formulation
spcSpace defined on the DtN boundary
DtNCoeffcoefficients of the DtN map

Definition at line 264 of file DtNmap2D.hh.

◆ addExactDtN_Circle2D() [2/4]

template<class F , class G >
void concepts::addExactDtN_Circle2D ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
Vector< Cmplx > &  rhs,
const ElementFormula< G > &  frm,
const Sequence< F >  DtNCoeffRhs 
)

Definition at line 336 of file DtNmap2D.hh.

◆ addExactDtN_Circle2D() [3/4]

void concepts::addExactDtN_Circle2D ( Matrix< Real > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< Real >  DtNCoeff 
)

Add DtN contribution for a circular boundary.

Parameters
destMatrix for the problem formulation
spcSpace defined on the DtN boundary
DtNCoeffcoefficients of the DtN map
Examples
exactDtN.cc.

Definition at line 223 of file DtNmap2D.hh.

◆ addExactDtN_Circle2D() [4/4]

void concepts::addExactDtN_Circle2D ( Matrix< Real > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< Real >  DtNCoeff,
Vector< Real > &  rhs,
const ElementFormula< Real > &  frm,
const Sequence< Real >  DtNCoeffRhs 
)

Definition at line 286 of file DtNmap2D.hh.

◆ addExactDtN_X_2D() [1/3]

template<class F >
void concepts::addExactDtN_X_2D ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 423 of file DtNmap2D.hh.

◆ addExactDtN_X_2D() [2/3]

template<class F , class G >
void concepts::addExactDtN_X_2D ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
Vector< Cmplx > &  rhs,
const ElementFormula< G > &  frm,
const Sequence< F >  DtNCoeffRhs,
const Real  L = 1.0 
)

Definition at line 447 of file DtNmap2D.hh.

◆ addExactDtN_X_2D() [3/3]

void concepts::addExactDtN_X_2D ( Matrix< Real > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< Real >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 373 of file DtNmap2D.hh.

◆ addExactDtN_X_2Dcos() [1/2]

template<class F >
void concepts::addExactDtN_X_2Dcos ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 700 of file DtNmap2D.hh.

◆ addExactDtN_X_2Dcos() [2/2]

template<class F , class G >
void concepts::addExactDtN_X_2Dcos ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
Vector< Cmplx > &  rhs,
const ElementFormula< G > &  frm,
const Sequence< F >  DtNCoeffRhs,
const Real  L = 1.0 
)

Definition at line 716 of file DtNmap2D.hh.

◆ addExactDtN_X_2Dcos_wp()

template<class F , class G >
void concepts::addExactDtN_X_2Dcos_wp ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
Vector< Cmplx > &  rhs,
const G &  frm,
const Sequence< F >  DtNCoeffRhs,
const Real  L = 1.0 
)

Definition at line 214 of file DtNmap2D_visc.hh.

◆ addExactDtN_X_2Dcossin() [1/2]

template<class F >
void concepts::addExactDtN_X_2Dcossin ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 794 of file DtNmap2D.hh.

◆ addExactDtN_X_2Dcossin() [2/2]

template<class F , class G >
void concepts::addExactDtN_X_2Dcossin ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
Vector< Cmplx > &  rhs,
const ElementFormula< G > &  frm,
const Sequence< F >  DtNCoeffRhs,
const Real  L = 1.0 
)

Definition at line 813 of file DtNmap2D.hh.

◆ addExactDtN_X_2Dcossin_wp()

template<class F , class G >
void concepts::addExactDtN_X_2Dcossin_wp ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
Vector< Cmplx > &  rhs,
const G &  frm,
const Sequence< F >  DtNCoeffRhs,
const Real  L = 1.0 
)

Definition at line 251 of file DtNmap2D_visc.hh.

◆ addExactDtN_X_2Dsin() [1/2]

template<class F >
void concepts::addExactDtN_X_2Dsin ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 737 of file DtNmap2D.hh.

◆ addExactDtN_X_2Dsin() [2/2]

template<class F , class G >
void concepts::addExactDtN_X_2Dsin ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
Vector< Cmplx > &  rhs,
const ElementFormula< G > &  frm,
const Sequence< F >  DtNCoeffRhs,
const Real  L = 1.0 
)

Definition at line 752 of file DtNmap2D.hh.

◆ addExactDtN_X_2Dsin_wp()

template<class F , class G >
void concepts::addExactDtN_X_2Dsin_wp ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
Vector< Cmplx > &  rhs,
const G &  frm,
const Sequence< F >  DtNCoeffRhs,
const Real  L = 1.0 
)

Definition at line 233 of file DtNmap2D_visc.hh.

◆ addExactDtN_X_2Dsincos() [1/2]

template<class F >
void concepts::addExactDtN_X_2Dsincos ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 837 of file DtNmap2D.hh.

◆ addExactDtN_X_2Dsincos() [2/2]

template<class F , class G >
void concepts::addExactDtN_X_2Dsincos ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
Vector< Cmplx > &  rhs,
const ElementFormula< G > &  frm,
const Sequence< F >  DtNCoeffRhs,
const Real  L = 1.0 
)

Definition at line 857 of file DtNmap2D.hh.

◆ addExactDtN_X_2Dsincos_wp()

template<class F , class G >
void concepts::addExactDtN_X_2Dsincos_wp ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
Vector< Cmplx > &  rhs,
const G &  frm,
const Sequence< F >  DtNCoeffRhs,
const Real  L = 1.0 
)

Definition at line 274 of file DtNmap2D_visc.hh.

◆ addExactDtN_X_2Dsym()

template<class F >
void concepts::addExactDtN_X_2Dsym ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 675 of file DtNmap2D.hh.

◆ addExactDtN_X_2Dunsym()

template<class F >
void concepts::addExactDtN_X_2Dunsym ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 772 of file DtNmap2D.hh.

◆ addExactDtN_Y_2D() [1/2]

template<class F >
void concepts::addExactDtN_Y_2D ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 488 of file DtNmap2D.hh.

◆ addExactDtN_Y_2D() [2/2]

template<class F , class G >
void concepts::addExactDtN_Y_2D ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
Vector< Cmplx > &  rhs,
const ElementFormula< G > &  frm,
const Sequence< F >  DtNCoeffRhs,
const Real  L = 1.0 
)

Definition at line 512 of file DtNmap2D.hh.

◆ addExactDtN_Y_2Dcos()

template<class F >
void concepts::addExactDtN_Y_2Dcos ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 578 of file DtNmap2D.hh.

◆ addExactDtN_Y_2Dcossin()

template<class F >
void concepts::addExactDtN_Y_2Dcossin ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 635 of file DtNmap2D.hh.

◆ addExactDtN_Y_2Dsin()

template<class F >
void concepts::addExactDtN_Y_2Dsin ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 596 of file DtNmap2D.hh.

◆ addExactDtN_Y_2Dsincos()

template<class F >
void concepts::addExactDtN_Y_2Dsincos ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 656 of file DtNmap2D.hh.

◆ addExactDtN_Y_2Dsym()

template<class F >
void concepts::addExactDtN_Y_2Dsym ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 553 of file DtNmap2D.hh.

◆ addExactDtN_Y_2Dunsym()

template<class F >
void concepts::addExactDtN_Y_2Dunsym ( Matrix< Cmplx > &  dest,
const SpaceOnCells< Real > &  spc,
const Sequence< F >  DtNCoeff,
const Real  L = 1.0 
)

Definition at line 613 of file DtNmap2D.hh.

◆ adjugate() [1/2]

template<class F , uint dim>
Mapping<F,dim> concepts::adjugate ( const Mapping< F, dim > &  m)

Definition at line 33 of file operations.hh.

◆ adjugate() [2/2]

template<class F , uint dim>
Mapping<F,dim>& concepts::adjugate ( Mapping< F, dim > &  m)

Definition at line 30 of file operations.hh.

◆ allConnectors() [1/2]

template<class F , class G >
Sequence<G*> concepts::allConnectors ( const F &  cntr,
G *(F::*)(uint) const  fun 
)

Return all connectors of a particular type of another connector, e.g.

all edges of a cell

Sequence<Connector1*> edges = allConnectors(cntr, &Connector2::edge);

Definition at line 126 of file connectorSequence.hh.

◆ allConnectors() [2/2]

template<class F , class G >
void concepts::allConnectors ( const F &  cntr,
G *(F::*)(uint) const  fun,
Set< G * > &  set 
)

Return all connectors of a particular type of another connector, e.g.

all edges of a cell

Set<Connector1*> edges;
allConnectors(cntr, &Connector2::edge, edges);

Definition at line 177 of file connectorSet.hh.

◆ apply()

template<class F , class H , class I >
void concepts::apply ( Operator< F > &  op,
const Matrix< H > &  mX,
Matrix< I > &  mY 
)

Multiplication with a matrix.

Decomposes matrix mX into vectors, apply standard application operator of op and adds(!) the resulting vectors to mY.

Author
Kersten Schmidt, 2005

Definition at line 256 of file matrix.hh.

◆ besselJ0()

Real concepts::besselJ0 ( const Real  x)

◆ besselJ1()

Real concepts::besselJ1 ( const Real  x)

◆ besselJn() [1/2]

Real concepts::besselJn ( const Real  x,
const int  n 
)

Evaluates the Bessel function $J_n(x)$.

◆ besselJn() [2/2]

Sequence< Real > concepts::besselJn ( const Real  x,
const Sequence< int > &  n 
)

Evaluates the Bessel function $J_n(x)$ for several orders.

Evaluates the Bessel function $ Y_n(x) $ for several orders.

◆ besselY0()

Real concepts::besselY0 ( const Real  x)

◆ besselY1()

Real concepts::besselY1 ( const Real  x)

◆ besselYn()

Real concepts::besselYn ( const Real  x,
const int  n 
)

Evaluates the Bessel function $ Y_n(x) $.

◆ buildEdgeMesh()

void concepts::buildEdgeMesh ( Scan2 *  sc,
const concepts::Set< uint >  attrib,
MutableMeshBase &  emsh 
)

Construct a mesh of edges of a 2D mesh w.r.t.

to particular attributes.

Parameters
scScanner over the cells of the 2D mesh.
attribSet of edge attributes.
emshEdge mesh to which the elements on the edge are added.

Currently work only for Quad2d as they are only provide a method to generate a cell for an edge.

Typical call 

concepts::MutableMesh1 edgeMsh;
concepts::Set<uint> eAttrib; eAttrib.insert(2);
concepts::buildEdgeMesh(msh.scan(), eAttrib, edgeMsh);

The mesh on edges takes over the parent-child relationship from the quadrilateral mesh. But, after construction the meshes are independent meaning that refinement in one mesh is not automatically followed by the other.

The topological objects (connectors) are hold outside, most probably by the 2D mesh which must consequently not be deleted.

Author
Kersten Schmidt, 2009

◆ chebychevPoints()

void concepts::chebychevPoints ( concepts::Array< Real > &  p)
inline

Zeros of Chebychev polynomials in [-1,1].

Number of points is given by the size of the array.

Definition at line 106 of file arrayOp.hh.

◆ cmplx_i()

const Cmplx concepts::cmplx_i ( 0  ,
1   
)

◆ componentArray()

template<class F , uint dim>
Array<F> concepts::componentArray ( const Array< Point< F, dim >> &  a,
uint  i 
)

Returns the component array of an array of vectors.

Parameters
icomponent

Definition at line 121 of file arrayOp.hh.

◆ computeKarniadakisValues()

const concepts::Array<Real> concepts::computeKarniadakisValues ( uint  np,
const Real *  absc,
uint  npx,
uint  type 
)
inline

Evaluate (transformed) Karniadakis Shapefunctions up to a order np on requested abcissa points in [0,1].

Per standard Karniadakis Shapefunctions are defined on [-1,1]. Here they are given analytical as polynomial transformed on [0,1].

This applicates as following: Let us say we want to evaluate the original shapefunction at the point -1 + eps. For too small eps, we observe cancellation effect due to mashine precision. As a consequence since almost all karniadakis polynomials are zero at -1, they will be evaluated as zero due to the cancelation effect. To avoid this, integration points are computed numerical stable on [0,1], with small values delta around 0. Now the analytical given shapefunctions on [0,1] can be evaluated close to zero, without mentionable cancellation effect.

Note that the second basis function, namely 1-x, as well like almost all derivatives are evaluated with cancellation effect near to zero.

Those evaluations are done by recursion formulas, directly derived from recursion formulas of the jacobian polynomials on [-1,1].

Parameters
npevaluate shapefuntions up to order np, i.e np+1 shapefunctions, that is for np=2 (1-x) x x(1-x)
abscabcissa points in [0,1], must be preallocated
npxnumber of abcissa points
type0 for Karniadakis<1, 0> normal 1 for Karniadakis<1, 1> derivative
Author
Robert Gruhlke, 2014

Definition at line 46 of file karniadakisOp.hh.

◆ convertCCS_rowSorting()

template<class F >
void concepts::convertCCS_rowSorting ( F &  m,
typename F::type *  a,
int *  asub,
int *  xa 
)

Method converts a matrix of type F to Sparse Column Storage (CCS) format.

The matrix type needs an iterator over the entrances, which moves at least row by row. Inside the row the entrances are sorted by column before writing to the output arrays.

Parameters
mmatrix
aarray of values
asubarray of row indices
xaarrays of column pointers
Author
, Kersten Schmidt, 2005

Definition at line 135 of file CRS.hh.

◆ convertCRS_rowSorting()

template<class F >
void concepts::convertCRS_rowSorting ( F &  m,
typename F::value_type *  a,
int *  asub,
int *  xa 
)

Method converts a matrix of type F to Sparse Row Storage (CRS) format.

The matrix type needs an iterator over the entrances, which moves at least row by row. Inside the row the entrances are sorted by column before writing to the output arrays.

Parameters
mmatrix
aarray of values
asubarray of column indices
xaarrays of row pointers
Author
, Kersten Schmidt, 2005

Definition at line 88 of file CRS.hh.

◆ convertIJK_unSorted()

template<class F >
void concepts::convertIJK_unSorted ( F &  m,
typename F::type *  a,
int *  irn,
int *  jcn 
)

Definition at line 171 of file CRS.hh.

◆ createBelosSolverMgr()

template<class T >
Teuchos::RCP< Belos::SolverManager<T, Tpetra::MultiVector<T, int>, Tpetra::Operator<T> > > concepts::createBelosSolverMgr ( std::string  solverType,
const Teuchos::RCP< Teuchos::ParameterList > &  solverParam,
Teuchos::RCP< Belos::LinearProblem< T, Tpetra::MultiVector< T, int >, Tpetra::Operator< T > > >  linearProblem 
)

Sets the solver type to one of the followings.

  • "GMRES"
  • "BLOCKCG"
  • "PSEUDOCG"

Definition at line 36 of file belosSolver_decl.hh.

◆ createIfpackPrec()

template<class T >
Teuchos::RCP<Ifpack2::Preconditioner<T> > concepts::createIfpackPrec ( std::string  precType,
Teuchos::RCP< Teuchos::ParameterList >  precParam,
const Teuchos::RCP< const Tpetra::CrsMatrix< T, int > >  A 
)

precType can assume the following parameters

  • "DIAGONAL"
  • "RELAXATION"
  • "CHEBYSHEV"
  • "ILUT"
  • "RILUK"

Definition at line 87 of file belosSolver_decl.hh.

◆ demangle()

std::string concepts::demangle ( const char *  name)

Returns the class name of a typeid name return statement.

This is a inbuild solution for the |c++filt -t option, when calling the program*

Parameters
nameName of the typeid
Remarks
If the compiler is not gcc, this function returns exactly std::string(name)
Author
Robert Gruhlke, Adrien Semin 2016

◆ determinant()

template<class F , uint dim>
F concepts::determinant ( const Mapping< F, dim > &  m)

Definition at line 27 of file operations.hh.

◆ ensureEnding()

std::string concepts::ensureEnding ( const std::string &  filename,
const std::string  ending 
)

Returns a string with particular ending.

Append it, if needed.

Author
Kersten Schmidt, 2005

◆ evaluatepermutation()

Real3d concepts::evaluatepermutation ( const Real3d  p,
const int  index 
)

Evaluation of a 3d permutation.

We consider the following evaluation conventions

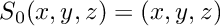
  • $S_0$ is the identity operator: $S_0(x,y,z) = (x,y,z)$
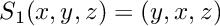
  • $S_1$ is the (x,y) swap operator: $S_1(x,y,z) = (y,x,z)$
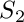  • $S_2$ is the (x,z) swap operator: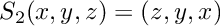 $S_2(x,y,z) = (z,y,x)$
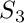  • $S_3$ is the (y,z) swap operator: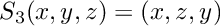 $S_3(x,y,z) = (x,z,y)$
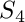  • $S_4$ is the (x,y,z) permutation operator: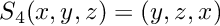 $S_4(x,y,z) = (y,z,x)$
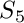  • $S_5$ is the (x,z,y) permutation operator: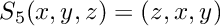 $S_5(x,y,z) = (z,x,y)$
Parameters
ppoint to evaluate
indexindex of the permutation

◆ exception_set_fields()

template<class exc >
exc concepts::exception_set_fields ( exc  e,
const std::string &  file,
const unsigned int  line,
const std::string &  function,
const std::string &  excName 
)

Sets fields on exception and throws it.

This routine does the main work for the conceptsException macro. This routine should not be called directly, it is used by the conceptsException macro.

Returns
An exception which can then be thrown
Parameters
eException to be thrown
fileFilename where the exception was thrown from
lineLine where the exception was thrown from
functionName of the function that threw the exception
excNameThe name of the exception
See also
conceptsException
ExceptionBase
Author
Philipp Frauenfelder, 2000

Definition at line 316 of file exceptions.hh.

◆ exception_throw_assert()

template<class exc >
void concepts::exception_throw_assert ( const std::string &  file,
int  line,
const std::string &  function,
const std::string &  exc_name,
const std::string &  cond,
exc  e 
)

Sets the fields of an assertion and throws it.

This routine does the main work for the exception generation mechanism used in the conceptsAssert macro. This routine should not be called directly, it is used by the conceptsAssert macro.

See also
conceptsAssert
Assertion
Author
Philipp Frauenfelder, 2000

Definition at line 364 of file exceptions.hh.

◆ g_fast()

Cmplx concepts::g_fast ( const Real  L,
const Real  omega,
const Real  c,
const Real  rho0,
const Real  nu,
const uint  j 
)

Compute the coefficients.

\[g_{j,f}\]

Definition at line 80 of file DtNmap2Dvisc.hh.

◆ g_slow()

Cmplx concepts::g_slow ( const Real  L,
const Real  omega,
const Real  c,
const Real  rho0,
const Real  nu,
const uint  j 
)

Compute the coefficients.

\[g_{j,s}\]

Definition at line 101 of file DtNmap2Dvisc.hh.

◆ GaussJacobiAbscWght()

void concepts::GaussJacobiAbscWght ( double *  x,
double *  w,
const uint  p 
)

Computes and returns the integration weights and abscissas for the Gauss Jacobi integration.

The abscissas no not include the endpoints -1 and 1.

Integration with the quadrature rule

\[ \int_{-1}^1 f(x) \, dx \approx \sum_{i=0}^p w_i f(x_i) \]

is exact for polynomials $f \in P_{2p+1}$.

The abscissas $x_i$ are the zeros of $P_{p+1}^{(0,0)}(x)$ and the weights are

\[w_i = \frac{2}{1-x_i^2} \left( \frac{d}{dx} \left. P^{(0,0)}_{p+1}(x) \right|_{x=x_i} \right)^{-2}.\]

Precondition
The space for the arrays x and w is allocated, size: p+1.
Author
Philipp Frauenfelder, 2001

◆ GaussLobattoAbscWght()

void concepts::GaussLobattoAbscWght ( double *  x,
double *  w,
const uint  p,
const uint  j = 0 
)

Computes and returns the integration weights and abscissas for the Gauss (Jacobi) Lobatto integration.

The Jacobi version can be chosen with a parameter. The abscissas include both endpoints, ie. 1 and -1.

Integration with the quadrature rule

\[ \int_{-1}^1 f(x) \, dx \approx \sum_{i=0}^p w_i f(x_i) \]

is exact for polynomials $f \in P_{2p-1}$. The Jacobi version integrates

\[ \int_{-1}^1 f(x) (1-x)^j \, dx \approx \sum_{i=0}^p w_i f(x_i) \]

exactly for $f \in P_{2p-1}$.

The abscissas $x_i$ are the zeros of $(1-x^2) P_{p-1}^{(1,1)}(x)$ and the weights are $w_i = 2/(p(p+1) (P_p^{(0,0)}(x_i))^2)$. For the Jacobi version, the abscissas are the zeros of $(1-x^2) P_{p-1}^{(1+j,1)}(x)$ and the weights are $w_i = 2^{1+j}/(p(p+1+j) (P_p^{(j,0)}(x_i))^2)$ and $w_p = (1+j) \cdot 2^{1+j}/(p(p+1+j) (P_p^{(j,0)}(x_i))^2)$.

Parameters
xOutput: the integration abscissas
wOutput: the integration weights
pOrder of the integration, p+1 points are computed
jThe Jacobi version of the integration rule is used if this is non-zero.
Precondition
The space for the arrays x and w is allocated, size: p+1.
Author
Philipp Frauenfelder, 2000

◆ GaussRadauAbscWght()

void concepts::GaussRadauAbscWght ( double *  x,
double *  w,
const uint  p,
const uint  j = 0 
)

Computes and returns the integration weights and abscissas for the Gauss Radau Jacobi integration.

The Jacobi version can be chosen with a parameter. The abscissas include only one endpoint: -1.

Integration with the quadrature rule

\[ \int_{-1}^1 f(x) \, dx \approx \sum_{i=0}^p w_i f(x_i) \]

is exact for polynomials $f \in P_{2p}$. The Jacobi version integrates

\[ \int_{-1}^1 f(x) (1-x)^j \, dx \approx \sum_{i=0}^p w_i f(x_i) \]

exactly for $f \in P_{2p}$.

The abscissas $x_i$ are the zeros of $(1+x) P_{p}^{(j,1)}(x)$ and the weights are $w_i = 2/((p+1)(p+1+j) (P_p^{(j,0)}(x_i))^2)$.

Parameters
xOutput: the integration abscissas
wOutput: the integration weights
pOrder of the integration, p+1 points are computed
jThe Jacobi version of the integration rule is used if this is non-zero.
Precondition
The space for the arrays x and w is allocated, size: p+1.
Author
Philipp Frauenfelder, 2001

◆ getChild()

template<uint dimC>
void concepts::getChild ( const typename JacobianCell< dimC >::cell &  cCell,
const Point< Real, dimC > &  eta,
const std::array< Real, std::size_t(dimC)>  x0,
const std::array< Real, std::size_t(dimC)>  xN,
const typename JacobianCell< dimC >::cell *&  cld 
)

Searches through the dichotomic tree cell hierachy to find the unique child cell that is defined via the local point eta in [0,1]^dimC.

Precondition
the coarse Cells children if existing are preallocated, and introduce pointers
eta is in [0,1]^dimC for speed up

◆ getDirectory()

std::string concepts::getDirectory ( const std::string  str)

Returns the directory of a given full filename.

◆ getFilename()

std::string concepts::getFilename ( const std::string  str)

Returns the filename (with ending) of a given full filename.

◆ getFilenamePrefix()

std::string concepts::getFilenamePrefix ( const std::string  str)

Returns the prefix of a given full filename, e.g.

. "example" for "~/example.dat".

◆ getHelmholtzDtNCoeff_Circle2D()

Sequence<Cmplx> concepts::getHelmholtzDtNCoeff_Circle2D ( const Real  omega,
const Real  R,
uint  N = 0 
)

Returns the coefficients for a non-local DtN map for the Helmholtz operator with frequency omega for a circular boundary of radius R which is truncated at order N.

Parameters
Lwidth of the boundary
Ntruncation order
Examples
exactDtN.cc.

Definition at line 39 of file DtNmap2D.hh.

◆ getHelmholtzDtNCoeff_Straight2D()

Sequence<Cmplx> concepts::getHelmholtzDtNCoeff_Straight2D ( const Real  omega,
const Real  L,
uint  N = 0 
)

Returns the coefficients for a non-local DtN map for the Helmholtz operator with frequency omega for a straight boundary of length L which is truncated at order N.

In the strip $[0,L]\times[0,\infty)$ the solution of $-\Delta u - \omega^2 u = 0$ can be written as

\[u(x,y) = a_0 \exp(k_0 y) + \sum_{n=1}^N \left( a_n \cos(2\pi n\frac{x}{L}) + b_n \sin(2\pi n\frac{x}{L})\right) \mathrm{e}^{k_n y} \]

with

\[ a_0 = \frac{1}{L}\int_{0}^L u(x',0) \mathrm{d}x', \\ a_n = \frac{2}{L}\int_{0}^L u(x',0) \cos(2\pi n\frac{x'}{L})\mathrm{d}x', \\ b_n = \frac{2}{L}\int_{0}^L u(x',0) \sin(2\pi n\frac{x'}{L})\mathrm{d}x', \\ k_n = \imath \sqrt{\omega^2 - \Big( \frac{n \pi}{L}\Big)^2}, \quad \omega > \frac{n \pi}{L}, \\ k_n = - \sqrt{\Big( \frac{n \pi}{L}\Big)^2 - \omega^2}, \quad \text{otherwise}. \]

The normal derivative at $y = 0$ is

\[ \partial_y u(x,0) = a_0 k_0 + \sum_{n=1}^N k_n \left( a_n \cos(2\pi n\frac{x}{L}) + b_n \sin(2\pi n\frac{x}{L})\right) \]

and so

\[ \int_0^L \partial_y u(x,0) v(x,0) \mathrm{d}x = \frac{k_0}{L} \int_0^L u(x',0) \mathrm{d}x' \int_0^L v(x,0) \mathrm{d}x + \sum_{n=1}^N \frac{k_n}{L}\left( 2\int_{0}^L u(x',0) \cos(2\pi n\frac{x'}{L})\mathrm{d}x' \int_{0}^L v(x ,0) \cos(2\pi n\frac{x }{L})\mathrm{d}x + 2\int_{0}^L u(x',0) \sin(2\pi n\frac{x'}{L})\mathrm{d}x' \int_{0}^L v(x ,0) \sin(2\pi n\frac{x }{L})\mathrm{d}x \right) \]

The factor 2 is used to have the same coefficients for an derivation with $\exp(2\pi i n \frac{x}{L})$.

Parameters
omegawave pulse
Lwidth of the boundary
Ntruncation order
Author
Kersten Schmidt, 2012

Definition at line 190 of file DtNmap2D.hh.

◆ getLaplaceDtNCoeff_Circle2D()

Sequence<Real> concepts::getLaplaceDtNCoeff_Circle2D ( const Real  R,
uint  N = 0 
)

Returns the coefficients for a non-local DtN map for the Laplace operator for a circular boundary of radius R which is truncated at order N.

Parameters
omegawave pulse
Lwidth of the boundary
Ntruncation order

Definition at line 61 of file DtNmap2D.hh.

◆ getLaplaceDtNCoeff_Straight2D()

Sequence<Real> concepts::getLaplaceDtNCoeff_Straight2D ( const Real  L,
uint  N = 0 
)

Returns the coefficients for a non-local DtN map for the Laplace operator for a straight boundary of length L which is truncated at order N.

In the strip $[0,L]\times[0,\infty)$ the solution of $-\Delta u = 0$ can be written as

\[u(x,y) = a_0 + \sum_{n=1}^N \left( a_n \cos(2\pi n\frac{x}{L}) + b_n \sin(2\pi n\frac{x}{L})\right) \mathrm{e}^{-2\pi n\frac{y}{L}} \]

with

\[ a_0 = \frac{1}{L}\int_{0}^L u(x',0) \mathrm{d}x' a_n = \frac{2}{L}\int_{0}^L u(x',0) \cos(2\pi n\frac{x'}{L})\mathrm{d}x',\\ b_n = \frac{2}{L}\int_{0}^L u(x',0) \sin(2\pi n\frac{x'}{L})\mathrm{d}x'. \]

The normal derivative at $y = 0$ is

\[ \partial_y u(x,0) = \sum_{n=1}^N -\frac{2\pi n}{L}\left( a_n \cos(2\pi n\frac{x}{L}) + b_n \sin(2\pi n\frac{x}{L})\right) \]

and so

\[ \int_0^L -\partial_y u(x,0) v(x,0) \mathrm{d}x = \sum_{n=1}^N \frac{2\pi n}{L^2}\left( 2\int_{0}^L u(x',0) \cos(2\pi n\frac{x'}{L})\mathrm{d}x' \int_{0}^L v(x ,0) \cos(2\pi n\frac{x }{L})\mathrm{d}x + 2\int_{0}^L u(x',0) \sin(2\pi n\frac{x'}{L})\mathrm{d}x' \int_{0}^L v(x ,0) \sin(2\pi n\frac{x }{L})\mathrm{d}x \right) \]

The factor 2 is used to have the same coefficients for an derivation with $\exp(2\pi i n \frac{x}{L})$.

Note, that as for the Laplace problem with pure Neumann boundary conditions the constant may not be defined (DtN coefficient for $a_0$ is zero) and has to be excluded by a mean zero condition.

Parameters
Lwidth of the boundary
Ntruncation order
Author
Kersten Schmidt, 2012

Definition at line 129 of file DtNmap2D.hh.

◆ getNSDtNCoeff_Straight2D_partDn()

Sequence<Cmplx> concepts::getNSDtNCoeff_Straight2D_partDn ( const Real  L,
const Real  omega,
const Real  c,
const Real  rho0,
const Real  nu,
uint  N = 0 
)

Definition at line 123 of file DtNmap2Dvisc.hh.

◆ getNSDtNCoeff_Straight2D_partDt()

Sequence<Cmplx> concepts::getNSDtNCoeff_Straight2D_partDt ( const Real  L,
const Real  omega,
const Real  c,
const Real  rho0,
const Real  nu,
uint  N = 1 
)

Definition at line 146 of file DtNmap2Dvisc.hh.

◆ getNSDtNCoeff_Straight2D_partDttilde()

Sequence<Cmplx> concepts::getNSDtNCoeff_Straight2D_partDttilde ( const Real  L,
const Real  omega,
const Real  c,
const Real  rho0,
const Real  nu,
uint  N = 1 
)

Definition at line 169 of file DtNmap2Dvisc.hh.

◆ getNSDtNCoeff_Straight2D_partRn()

Sequence<Cmplx> concepts::getNSDtNCoeff_Straight2D_partRn ( const Real  L,
const Real  omega,
const Real  c,
const Real  rho0,
const Real  nu,
uint  N = 1 
)

Definition at line 191 of file DtNmap2Dvisc.hh.

◆ getNSDtNCoeff_Straight2D_partRntilde()

Sequence<Cmplx> concepts::getNSDtNCoeff_Straight2D_partRntilde ( const Real  L,
const Real  omega,
const Real  c,
const Real  rho0,
const Real  nu,
uint  N = 1 
)

Definition at line 214 of file DtNmap2Dvisc.hh.

◆ getNSDtNCoeff_Straight2D_partRt()

Sequence<Cmplx> concepts::getNSDtNCoeff_Straight2D_partRt ( const Real  L,
const Real  omega,
const Real  c,
const Real  rho0,
const Real  nu,
uint  N = 0 
)

Definition at line 236 of file DtNmap2Dvisc.hh.

◆ getNumberofRows() [1/2]

template<class F >
uint concepts::getNumberofRows ( F &  m)

Definition at line 242 of file matrix.hh.

◆ getNumberofRows() [2/2]

template<class F >
uint concepts::getNumberofRows ( HashedSparseMatrix< F > &  m)

Definition at line 275 of file hashedSMatrix.hh.

◆ hankel_1_deriv_n() [1/2]

Cmplx concepts::hankel_1_deriv_n ( const Real  x,
const int  n 
)

Evaluates the derivative $ H^{(1)}_n{}'(x) $ of the Hankel function $ H^{(1)}_n(x) = J_n(x) + \mathrm{i}Y_n(x) $.

◆ hankel_1_deriv_n() [2/2]

Sequence<Cmplx> concepts::hankel_1_deriv_n ( const Real  x,
const Sequence< int > &  n 
)

◆ hankel_1_n() [1/2]

Cmplx concepts::hankel_1_n ( const Real  x,
const int  n 
)

Evaluates the Hankel function $ H^{(1)}_n(x) = J_n(x) + \mathrm{i}Y_n(x) $.

◆ hankel_1_n() [2/2]

Sequence<Cmplx> concepts::hankel_1_n ( const Real  x,
const Sequence< int > &  n 
)

◆ hankel_2_deriv_n() [1/2]

Cmplx concepts::hankel_2_deriv_n ( const Real  x,
const int  n 
)

Evaluates the derivative $ H^{(2)}_n{}'(x) $ of the Hankel function $ H^{(2)}_n(x) = J_n(x) - \mathrm{i}Y_n(x) $.

◆ hankel_2_deriv_n() [2/2]

Sequence<Cmplx> concepts::hankel_2_deriv_n ( const Real  x,
const Sequence< int > &  n 
)

◆ hankel_2_n() [1/2]

Cmplx concepts::hankel_2_n ( const Real  x,
const int  n 
)

Evaluates the Hankel function $ H^{(2)}_n(x) = J_n(x) - \mathrm{i}Y_n(x) $.

◆ hankel_2_n() [2/2]

Sequence<Cmplx> concepts::hankel_2_n ( const Real  x,
const Sequence< int > &  n 
)

◆ import2dMeshGeneralFromInput()

Import2dMeshGeneral* concepts::import2dMeshGeneralFromInput ( const InOutParameters  input,
bool  verbose = false 
)

Loads a mesh from a paramater list.

The parameter list needs the strings: "inputfilename" - prefix for all file names.

The parameter list may include the strings: "inputpath" - name of the path where the files are inside. If not given, the current working directory (".") is taken.

It will be excepted five files, namely the coordinate, the element, the attribute, the edge radia and the edge correlation file of the following names. Let the prefix be "example". Then, the files are "example_Coord.dat", "example_Elms.dat", "example_Attr.dat", "example_EdgRadia.dat", "example_EdgCorr.dat".

The files have to exist, but may be empty.

Author
Kersten Schmidt, 2009
Examples
cig_load_input_data.cc, and elasticity2D_tutorial.cc.

◆ integrate() [1/6]

template<typename G >
Real concepts::integrate ( const Element< G > &  elm)

Returns the area of the cell belonging to the element elm.

Author
Kersten Schmidt, 2005

Definition at line 43 of file integral.hh.

◆ integrate() [2/6]

template<typename F , typename G >
F concepts::integrate ( const ElementWithCell< G > &  elm,
const ElementFormula< F, G > &  frm,
const Real  t = 0.0,
IntegrationCell::intFormType  form = IntegrationCell::ZERO 
)

Returns the integral of the element formula frm over the cell belonging to the element elm.

Author
Kersten Schmidt, 2005

Definition at line 64 of file integral.hh.

◆ integrate() [3/6]

template<class F , class G >
F concepts::integrate ( const ElementWithCell< G > &  elm1,
const ElementWithCell< G > &  elm2,
const ElementFormula< F, G > &  frm1,
const ElementFormula< F, G > &  frm2,
const Real  t = 0,
IntegrationCell::intFormType  form = IntegrationCell::ZERO 
)

Returns the integral over the element elm1 respective elm2 of the product of the ElementFormulas frm1 and frm2.

The two elements must use the same topological cells.

Author
Philipp Kliewe, 2013

Definition at line 154 of file integral.hh.

◆ integrate() [4/6]

template<class F , typename G >
F concepts::integrate ( const Sequence< ElementWithCell< G > * > &  elm_seq,
const ElementFormula< F, G > &  frm,
const Real  t = 0.0,
IntegrationCell::intFormType  form = IntegrationCell::ZERO 
)

Returns the integral over elements in sequence elm_seq of the formula or element formula frm at time t.

The integration form is form.

Cells are valid, if they are derivated from IntegrationCell.

See also
IntegrationCell
Author
Maxim Felde, 2015

Definition at line 131 of file integral.hh.

◆ integrate() [5/6]

template<class F , typename G >
F concepts::integrate ( const SpaceOnCells< G > &  spc,
const ElementFormula< F, G > &  frm,
const Real  t = 0.0,
IntegrationCell::intFormType  form = IntegrationCell::ZERO 
)

Returns the integral over space spc of the formula or element formula frm at time t.

The integration form is form.

Spaces are valid, if their elements are derivated from IntegrationCell.

See also
IntegrationCell
Author
Kersten Schmidt, 2005

Definition at line 96 of file integral.hh.

◆ integrate() [6/6]

template<class F , class G >
F concepts::integrate ( const SpaceOnCells< G > &  spc1,
const SpaceOnCells< G > &  spc2,
const ElementFormula< F, G > &  frm1,
const ElementFormula< F, G > &  frm2,
const Real  t = 0,
IntegrationCell::intFormType  form = IntegrationCell::ZERO 
)

Returns the integral over spc1 respective spc2 of the product of the ElementFormulas frm1 and frm2, where frm1 is given on spc1 and frm2 is given on spc2.

The two spaces must use the same topological cells. This method can be used for integrals over interfaces.

Author
Philipp Kliewe, 2013

Definition at line 182 of file integral.hh.

◆ inverse() [1/4]

template<class F >
F concepts::inverse ( const F &  f)

Definition at line 18 of file operations.hh.

◆ inverse() [2/4]

template<class F , uint dim>
Mapping<F,dim> concepts::inverse ( const Mapping< F, dim > &  m)

Definition at line 24 of file operations.hh.

◆ inverse() [3/4]

template<class F >
F& concepts::inverse ( F &  f)

Definition at line 15 of file operations.hh.

◆ inverse() [4/4]

template<class F , uint dim>
Mapping<F,dim>& concepts::inverse ( Mapping< F, dim > &  m)

Definition at line 21 of file operations.hh.

◆ isParallelRunning()

bool concepts::isParallelRunning ( )

Tests if the instruction MPI::Init() was called.

Remarks
This method can also be called in sequential compiling, therefore will always return false
Author
Adrien Semin, 2016

◆ jacobianDeterminant() [1/2]

Array<Real> concepts::jacobianDeterminant ( const Hexahedron3d &  Hexa,
const Array< QuadratureRule1d * > &  ArrayQuad1D 
)

Computes a multi-dimensional Jacobian determinant tensor.

Parameters
Hexamapped hexahedron to consider
ArrayQuad1Dpointers to 1D quadratures
Author
Adrien Semin, 2015

◆ jacobianDeterminant() [2/2]

Real concepts::jacobianDeterminant ( const Hexahedron3d &  Hexa,
const Real3d &  xi 
)

Computes the Jacobian determinant $J_K = \text{det}(dF_K)$.

Parameters
Hexamapped hexahedron to consider
xireference element in the cube 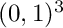$(0,1)^3$
Author
Adrien Semin, 2015

◆ jacobianTensor() [1/2]

Array<Mapping<Real, 3, 3> > concepts::jacobianTensor ( const Hexahedron3d &  Hexa,
const Array< QuadratureRule1d * > &  ArrayQuad1D 
)

Computes a multi-dimensional Jacobian tensor.

Parameters
Hexamapped hexahedron to consider
ArrayQuad1Dpointers to 1D quadratures
Author
Adrien Semin, 2015

◆ jacobianTensor() [2/2]

Mapping<Real, 3, 3> concepts::jacobianTensor ( const Hexahedron3d &  Hexa,
const Real3d &  xi 
)

Compute the Jacobian tensor $dF_K$ that goes from a reference element $\xi \in (0,1)^3$ to M(3,3)

Parameters
Hexamapped hexahedron to consider
xireference element in the cube 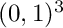$(0,1)^3$
Author
Adrien Semin, 2015

◆ JacobiDerivatives()

void concepts::JacobiDerivatives ( const double  alf,
const double  bet,
const int  maxn,
const double *  x,
const int  m,
const double *  p,
double *  q 
)

Computes the values of the derivatives of the Jacobi polynomials.

$\frac{d}{dx} P^{(\alpha,\beta)}_i (x_j)$ for $i = 0, \dots, maxn$ and $x_j \in x$, $|x| = m$.

Parameters
alf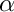$\alpha$
bet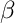$\beta$
maxnHighest polynomial degree to be computed
xArray of size m with the points in which the polynomials should be evaluated. $x_j \in [-1,1]$.
mSize of array x
pArray of the size m*(maxn+1) filled with the Jacobi polynomials.
qArray of the size m*(maxn+1) (must be allocated), will be filled with the values of the derivatives of the poynomials in the points with i running fastest.
Precondition
The space for the array q is allocated, size: m*(maxn+1)
Author
Philipp Frauenfelder, after the recursion formulae in Karniadakis / Sherwin "Spectral/hp Element Methods for CFD" p. 350f

◆ JacobiPol()

void concepts::JacobiPol ( const double  alf,
const double  bet,
const int  maxn,
const double *  x,
const int  m,
double *  p 
)

Computes the values of the Jacobi polynomials.

$P^{(\alpha, \beta)}_i (x_j)$ for $i = 0, \dots, maxn$ and $x_j \in x$, $|x| = m$.

Parameters
alf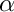$\alpha$
bet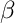$\beta$
maxnHighest polynomial degree to be computed
xArray of size m with the points in which the polynomials should be evaluated. $x_j \in [-1,1]$.
mSize of array x
pArray of the size m*(maxn+1) (must be allocated), will be filled with the values of the poynomials in the points with i running fastest.
Precondition
The space for the array p is allocated, size: m*(maxn+1)
Author
Philipp Frauenfelder, after the recursion formulae in Karniadakis / Sherwin "Spectral/hp Element Methods for CFD" p. 350f

◆ JacobiZeros()

void concepts::JacobiZeros ( double *  x,
int  p,
double  alf,
double  bet 
)

Computes the zeros of the Jacobi polynomials $P_{p}^{(\alpha,\beta)}(x)$.

Parameters
xOutput: the zeros of the Jacobi polynomials in the elements 1, ..., p. The element 0 of the array is untouched.
pDegree of the Jacobi polynomial
alf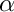$\alpha$
bet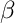$\beta$
Precondition
The space for the arrays x is allocated, size: p+1
Author
(C) Copr. 1986-92 Numerical Recipes Software VsXz&52.!-.

◆ L2product() [1/3]

template<typename F , typename G >
Real concepts::L2product ( const ElementWithCell< G > &  elm,
const ElementFormula< F, G > &  u,
const ElementFormula< Real > *  c = 0,
const Real  t = 0.0,
IntegrationCell::intFormType  form = IntegrationCell::ZERO 
)

Returns the L2 product or with c weighted L2 product of an element formula u over the cell belonging to the element elm.

\[\int\limits_{K}c u^\top\cdot\overline{u}\,dx\]

Author
Kersten Schmidt, 2005
Examples
parallelizationTutorial.cc.

Definition at line 214 of file integral.hh.

◆ L2product() [2/3]

template<class F , typename G >
Real concepts::L2product ( const Sequence< ElementWithCell< G > * > &  elm_seq,
const ElementFormula< F, G > &  u,
const ElementFormula< Real > *  c = 0,
const Real  t = 0.0,
IntegrationCell::intFormType  form = IntegrationCell::ZERO 
)

Returns the L2 product or with c weighted L2 product of an element formula u over the cells belonging to the elements in the sequence elm_seq.

\[\int\limits_{K}c u^\top\cdot\overline{u}\,dx\]

Author
Maxim Felde, 2015

Definition at line 296 of file integral.hh.

◆ L2product() [3/3]

template<class F , typename G >
Real concepts::L2product ( SpaceOnCells< F > &  spc,
const G &  u,
const ElementFormula< Real > *  c = 0,
const Real  t = 0.0,
IntegrationCell::intFormType  form = IntegrationCell::ZERO 
)

Returns the L2 product or with c weighted L2 product over space spc of the formula or element formula u at time t.

The integration form is form.

\[\int\limits_{\Omega}c u^\top\cdot\overline{u}\,dx\]

Spaces are valid, if their elements are derivated from IntegrationCell.

See also
IntegrationCell
Author
Kersten Schmidt, 2005

Definition at line 267 of file integral.hh.

◆ lambda_j_fast()

Cmplx concepts::lambda_j_fast ( const Real  L,
const Real  omega,
const Real  c,
const Real  rho0,
const Real  nu,
const uint  j 
)

Compute the eigenvalues.

\[\lambda_{j,f}\]

Definition at line 30 of file DtNmap2Dvisc.hh.

◆ lambda_j_slow()

Cmplx concepts::lambda_j_slow ( const Real  L,
const Real  omega,
const Real  c,
const Real  rho0,
const Real  nu,
const uint  j 
)

Compute the eigenvalues.

\[\lambda_{j,s}\]

Definition at line 55 of file DtNmap2Dvisc.hh.

◆ lambda_limit()

Cmplx concepts::lambda_limit ( const Real  omega,
const Real  c0,
const int  n,
const Real  L 
)

Definition at line 82 of file DtNmap2D_visc.hh.

◆ makeAdaptiveQuadrature()

template<class FunctionT >
std::shared_ptr<const FunctionT> concepts::makeAdaptiveQuadrature ( const uint  nQuadraturePoints,
const intRule  quadratureType 
)

factory function encapsulating the memory manager

FIXME: code factorization

Definition at line 191 of file flyweight.hh.

◆ makeArray() [1/4]

template<class F , class G >
void concepts::makeArray ( const F &  cell,
const Array< Real > &  p,
G(F::*)(Real) const  fun,
Array< G > &  array 
)

Creates an array array by applying an function fun of a cell cell for each value p.

Author
Kersten Schmidt, 2009

Definition at line 24 of file arrays.hh.

◆ makeArray() [2/4]

template<class F , class G >
void concepts::makeArray ( const F &  cell,
const Array< Real > &  pX,
const Array< Real > &  pY,
const Array< Real > &  pZ,
G(F::*)(Real, Real, Real) const  fun,
Array< G > &  array,
bool  istensor = true 
)

Creates an array array by applying an function fun of a cell cell for each combination of the values pX and pY.

The fast loop is over pY for tensor basis case.

Also for non tensor case, there is one loop over all integration points (pX(i), pY(i)), i = 0,..., #points.

Author
Kersten Schmidt, 2009

Definition at line 79 of file arrays.hh.

◆ makeArray() [3/4]

template<class F , class G >
void concepts::makeArray ( const F &  cell,
const Array< Real > &  pX,
const Array< Real > &  pY,
G(F::*)(Real, Real) const  fun,
Array< G > &  array,
bool  istensor = true 
)

Creates an array array by applying an function fun of a cell cell for each combination of the values pX and pY.

The fast loop is over pY for tensor basis case.

Also for non tensor case, there is one loop over all integration points (pX(i), pY(i)), i = 0,..., #points.

Author
Kersten Schmidt, 2009

Definition at line 43 of file arrays.hh.

◆ makeArray() [4/4]

template<class F >
Array<F> concepts::makeArray ( std::initializer_list< F >  list)

Creates an array from a comma separated list of values.

For example, 

makeArray<int>({2, 3, 6, 7})

creates an array of 4 elements containing [2, 3, 6, 7].

Definition at line 90 of file arrayOp.hh.

◆ makecRCP_weak()

template<class T >
RCP< const T > concepts::makecRCP_weak ( T *  x)

Definition at line 129 of file sharedPointer_boost.hh.

◆ makeEquidistantSequence()

template<class F >
Sequence<F> concepts::makeEquidistantSequence ( uint  n,
const F &  first,
const F &  diff 
)

Definition at line 407 of file sequence.hh.

◆ makeQuadrature()

template<class FunctionT >
std::shared_ptr<const FunctionT> concepts::makeQuadrature ( const uint  nQuadraturePoints,
const intRule  quadratureType 
)

factory function encapsulating the memory manager

Bring here a polymorphic constructor

Definition at line 154 of file flyweight.hh.

◆ makeRangeSequence() [1/3]

Sequence<int> concepts::makeRangeSequence ( int  start,
int  afterlast 
)

Returns the sequence start, start+1,...,afterlast-1.

◆ makeRangeSequence() [2/3]

Sequence<int> concepts::makeRangeSequence ( int  start,
int  afterlast,
uint  dist 
)

Returns the sequence start, start+dist,...

such that last entry is smaller than afterlast

◆ makeRangeSequence() [3/3]

Sequence<int> concepts::makeRangeSequence ( uint  n)

Returns the sequence 0,1,...,n-1.

◆ makeRCP()

template<class T >
RCP< T > concepts::makeRCP ( T *  x)

Function to create a RCP which deletes the object when no RCP points on it anymore.

The function has to be used, if the object is created with new.

For example: 

RCP<int>::Type iP = makeRCP(new int(2));
iP.reset();   // deletes the integer 2

Second example: 

RCP<int>::Type iP = makeRCP(new int(3)), jP = iP;
jP.reset();   // does not delete the integer 3, as jP points still on it
iP.reset();   // deletes the integer 3, no RCP points on it

Definition at line 102 of file sharedPointer_boost.hh.

◆ makeRCP_weak()

template<class T >
RCP< T > concepts::makeRCP_weak ( T *  x)

Function to create a RCP without deleting the object in the destructor.

The function has to be used, if the object remains externally, e.g., in the heap.

For example: 

int i = 1;
RCP<int>::Type iP = makeRCP_weak(&i);
iP.reset();   // will not delete the integer 1

Definition at line 122 of file sharedPointer_boost.hh.

◆ makeSequence() [1/2]

template<class F >
Sequence<F> concepts::makeSequence ( std::initializer_list< F >  list)

Creates an sequence of length
from a comma separated list of values.

e.g. 

makeSequence(2, 3, 6, 7)

creates an sequence [2, 3, 6, 7]

Definition at line 395 of file sequence.hh.

◆ makeSequence() [2/2]

template<class F >
Sequence<F> concepts::makeSequence ( uint  n,
const F &  first,
  ... 
)

Creates an sequence of length
from a comma separated list of values.

e.g. 

makeSequence(4, 2, 3, 6, 7)

creates an sequence [2, 3, 6, 7]

Definition at line 375 of file sequence.hh.

◆ makeSet() [1/2]

template<class F >
Set<F> concepts::makeSet ( std::initializer_list< F >  list)

Creates an array from a comma separated list of values.

e.g. 

makeSet({3, 2, 6, 7})

creates an set [2, 3, 6, 7]

Definition at line 339 of file set.hh.

◆ makeSet() [2/2]

template<class F >
Set<F> concepts::makeSet ( uint  n,
const F &  first,
  ... 
)

Creates an array of length
from a comma separated list of values.

e.g. 

makeSet(4, 3, 2, 6, 7)

creates an set [2, 3, 6, 7]

Definition at line 320 of file set.hh.

◆ makeShapeFunction()

template<class FunctionT >
std::shared_ptr<const FunctionT> concepts::makeShapeFunction ( const concepts::QuadratureRule1d &  quadratureRule,
const uint  polynomialDegree 
)

factory function encapsulating the memory manager

Definition at line 122 of file flyweight.hh.

◆ match()

int concepts::match ( const Connector1 &  edg0,
const Connector1 &  edg1,
int  idx[] 
)

Checks, if two edges has a common vertex.

In that case the value 1 is returned, and the idx[0]-th vertex of edg0 coincide with the idx[1]-th vertex of edg1.

◆ matrixMultiplyRowSorting()

template<class F , class G , class H >
void concepts::matrixMultiplyRowSorting ( const F &  factL,
const G &  factR,
Matrix< H > &  dest 
)

Multiplies two matrices, which deliver at least a row sorted iterator, and adds (!) the result to a third matrix.

The matrices factL and factR needs the methods nofRows(), nofCols(), begin(row) or begin() respectivly.

Author
Kersten Schmidt, 2005

Definition at line 28 of file matrixMult.hh.

◆ memorycpy()

template<typename F , typename G >
void concepts::memorycpy ( F *  dest,
const G *  src,
size_t  n 
)

Copies n entries from src to dest (faster than std::memcpy)

Definition at line 31 of file vectorsMatrices.hh.

◆ newField()

template<class F >
F* concepts::newField ( uint  nr)
inline

Reserve memory for a field of type F and returns the pointer to first entrance.

Author
Kersten Schmidt, 2005

Definition at line 17 of file memory.hh.

◆ operator!=() [1/2]

template<class _Tp , class _Ref , class _Ptr >
bool concepts::operator!= ( const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &  __x,
const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &  __y 
)
inline

Definition at line 150 of file matrixIterator.hh.

◆ operator!=() [2/2]

template<class _Tp , class _RefL , class _PtrL , class _RefR , class _PtrR >
bool concepts::operator!= ( const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &  __x,
const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &  __y 
)
inline

Definition at line 158 of file matrixIterator.hh.

◆ operator*() [1/76]

BilinearFormContainer<Cmplx> concepts::operator* ( const BilinearFormContainer< Cmplx >  frm1,
const Cmplx  w 
)

◆ operator*() [2/76]

BilinearFormContainer<Cmplx> concepts::operator* ( const BilinearFormContainer< Cmplx >  frm1,
const Real  w 
)

◆ operator*() [3/76]

BilinearFormContainer<Cmplx> concepts::operator* ( const BilinearFormContainer< Real >  frm1,
const Cmplx  w 
)

◆ operator*() [4/76]

BilinearFormContainer<Real> concepts::operator* ( const BilinearFormContainer< Real >  frm1,
const Real  w 
)

Simple multiplication from right.

◆ operator*() [5/76]

ElementFormulaContainer<MapCmplx2d> concepts::operator* ( const Cmplx  a,
const ElementFormulaContainer< MapCmplx2d >  frm 
)

◆ operator*() [6/76]

ElementFormulaContainer<MapCmplx2d> concepts::operator* ( const Cmplx  a,
const ElementFormulaContainer< MapReal2d >  frm 
)

◆ operator*() [7/76]

BilinearFormContainer<Cmplx> concepts::operator* ( const Cmplx  w,
const BilinearFormContainer< Cmplx >  frm1 
)

◆ operator*() [8/76]

BilinearFormContainer<Cmplx> concepts::operator* ( const Cmplx  w,
const BilinearFormContainer< Real >  frm1 
)

◆ operator*() [9/76]

template<class F , uint dim>
Point<typename Combtype<F,Cmplx>::type,dim> concepts::operator* ( const Cmplx  x,
const Point< F, dim > &  y 
)
inline

Definition at line 246 of file vectorsMatrices.hh.

◆ operator*() [10/76]

template<class F , class G >
concepts::Array<typename Combtype<F,G>::type> concepts::operator* ( const concepts::Array< F > &  array,
const G &  val 
)

Multiplication operator.

Returns the product of an array of type F and a value of type G.

Definition at line 360 of file array.hh.

◆ operator*() [11/76]

ElementFormulaContainer<Cmplx> concepts::operator* ( const ElementFormulaContainer< Cmplx >  frm,
const Cmplx  a 
)

◆ operator*() [12/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< Cmplx >  frm,
const Cmplx2d  a 
)

◆ operator*() [13/76]

ElementFormulaContainer<Cmplx> concepts::operator* ( const ElementFormulaContainer< Cmplx >  frm,
const Real  a 
)

◆ operator*() [14/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< Cmplx >  frm,
const Real2d  a 
)

◆ operator*() [15/76]

ElementFormulaContainer<Cmplx> concepts::operator* ( const ElementFormulaContainer< Cmplx >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator*() [16/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< Cmplx >  frm1,
const ElementFormulaContainer< Cmplx2d >  frm2 
)

◆ operator*() [17/76]

ElementFormulaContainer<MapCmplx2d> concepts::operator* ( const ElementFormulaContainer< Cmplx >  frm1,
const ElementFormulaContainer< MapCmplx2d >  frm2 
)

◆ operator*() [18/76]

ElementFormulaContainer<MapCmplx2d> concepts::operator* ( const ElementFormulaContainer< Cmplx >  frm1,
const ElementFormulaContainer< MapReal2d >  frm2 
)

◆ operator*() [19/76]

ElementFormulaContainer<Cmplx> concepts::operator* ( const ElementFormulaContainer< Cmplx >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

◆ operator*() [20/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< Cmplx >  frm1,
const ElementFormulaContainer< Real2d >  frm2 
)

◆ operator*() [21/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< Cmplx2d >  frm,
const Cmplx  a 
)

◆ operator*() [22/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< Cmplx2d >  frm,
const Real  a 
)

◆ operator*() [23/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< Cmplx2d >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator*() [24/76]

ElementFormulaContainer<Cmplx> concepts::operator* ( const ElementFormulaContainer< Cmplx2d >  frm1,
const ElementFormulaContainer< Cmplx2d >  frm2 
)

◆ operator*() [25/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< Cmplx2d >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

◆ operator*() [26/76]

ElementFormulaContainer<Cmplx> concepts::operator* ( const ElementFormulaContainer< Cmplx2d >  frm1,
const ElementFormulaContainer< Real2d >  frm2 
)

◆ operator*() [27/76]

ElementFormulaContainer<MapCmplx2d> concepts::operator* ( const ElementFormulaContainer< MapCmplx2d >  frm,
const Cmplx  a 
)

◆ operator*() [28/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< MapCmplx2d >  frm,
const Cmplx2d  a 
)

◆ operator*() [29/76]

ElementFormulaContainer<MapCmplx2d> concepts::operator* ( const ElementFormulaContainer< MapCmplx2d >  frm,
const Real  a 
)

◆ operator*() [30/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< MapCmplx2d >  frm,
const Real2d  a 
)

◆ operator*() [31/76]

ElementFormulaContainer<MapCmplx2d> concepts::operator* ( const ElementFormulaContainer< MapCmplx2d >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator*() [32/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< MapCmplx2d >  frm1,
const ElementFormulaContainer< Cmplx2d >  frm2 
)

◆ operator*() [33/76]

ElementFormulaContainer<MapCmplx2d> concepts::operator* ( const ElementFormulaContainer< MapCmplx2d >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

◆ operator*() [34/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< MapCmplx2d >  frm1,
const ElementFormulaContainer< Real2d >  frm2 
)

◆ operator*() [35/76]

ElementFormulaContainer<MapCmplx2d> concepts::operator* ( const ElementFormulaContainer< MapReal2d >  frm,
const Cmplx  a 
)

◆ operator*() [36/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< MapReal2d >  frm,
const Cmplx2d  a 
)

◆ operator*() [37/76]

ElementFormulaContainer<MapReal2d> concepts::operator* ( const ElementFormulaContainer< MapReal2d >  frm,
const Real  a 
)

◆ operator*() [38/76]

ElementFormulaContainer<Real2d> concepts::operator* ( const ElementFormulaContainer< MapReal2d >  frm,
const Real2d  a 
)

◆ operator*() [39/76]

ElementFormulaContainer<MapCmplx2d> concepts::operator* ( const ElementFormulaContainer< MapReal2d >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator*() [40/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< MapReal2d >  frm1,
const ElementFormulaContainer< Cmplx2d >  frm2 
)

◆ operator*() [41/76]

ElementFormulaContainer<MapReal2d> concepts::operator* ( const ElementFormulaContainer< MapReal2d >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

◆ operator*() [42/76]

ElementFormulaContainer<Real2d> concepts::operator* ( const ElementFormulaContainer< MapReal2d >  frm1,
const ElementFormulaContainer< Real2d >  frm2 
)

◆ operator*() [43/76]

ElementFormulaContainer<Cmplx> concepts::operator* ( const ElementFormulaContainer< Real >  frm,
const Cmplx  a 
)

◆ operator*() [44/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< Real >  frm,
const Cmplx2d  a 
)

◆ operator*() [45/76]

ElementFormulaContainer<Real> concepts::operator* ( const ElementFormulaContainer< Real >  frm,
const Real  a 
)

Simple multiplying of a element formulas by a constant via *-operator.

◆ operator*() [46/76]

ElementFormulaContainer<Real2d> concepts::operator* ( const ElementFormulaContainer< Real >  frm,
const Real2d  a 
)

◆ operator*() [47/76]

ElementFormulaContainer<Cmplx> concepts::operator* ( const ElementFormulaContainer< Real >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator*() [48/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< Real >  frm1,
const ElementFormulaContainer< Cmplx2d >  frm2 
)

◆ operator*() [49/76]

ElementFormulaContainer<MapCmplx2d> concepts::operator* ( const ElementFormulaContainer< Real >  frm1,
const ElementFormulaContainer< MapCmplx2d >  frm2 
)

◆ operator*() [50/76]

ElementFormulaContainer<MapReal2d> concepts::operator* ( const ElementFormulaContainer< Real >  frm1,
const ElementFormulaContainer< MapReal2d >  frm2 
)

◆ operator*() [51/76]

ElementFormulaContainer<Real> concepts::operator* ( const ElementFormulaContainer< Real >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

Simple multiplying of two element formulas by *-operator.

◆ operator*() [52/76]

ElementFormulaContainer<Real2d> concepts::operator* ( const ElementFormulaContainer< Real >  frm1,
const ElementFormulaContainer< Real2d >  frm2 
)

◆ operator*() [53/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< Real2d >  frm,
const Cmplx  a 
)

◆ operator*() [54/76]

ElementFormulaContainer<Real2d> concepts::operator* ( const ElementFormulaContainer< Real2d >  frm,
const Real  a 
)

◆ operator*() [55/76]

ElementFormulaContainer<Cmplx2d> concepts::operator* ( const ElementFormulaContainer< Real2d >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator*() [56/76]

ElementFormulaContainer<Cmplx> concepts::operator* ( const ElementFormulaContainer< Real2d >  frm1,
const ElementFormulaContainer< Cmplx2d >  frm2 
)

◆ operator*() [57/76]

ElementFormulaContainer<Real2d> concepts::operator* ( const ElementFormulaContainer< Real2d >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

◆ operator*() [58/76]

ElementFormulaContainer<Real> concepts::operator* ( const ElementFormulaContainer< Real2d >  frm1,
const ElementFormulaContainer< Real2d >  frm2 
)

◆ operator*() [59/76]

Frm_Product<Cmplx> concepts::operator* ( const Formula< Cmplx > &  frm,
const Cmplx  a 
)

◆ operator*() [60/76]

Frm_Product<Cmplx,Cmplx,Real> concepts::operator* ( const Formula< Cmplx > &  frm,
const Real  a 
)

◆ operator*() [61/76]

Frm_Product<Cmplx> concepts::operator* ( const Formula< Cmplx > &  frm1,
const Formula< Cmplx > &  frm2 
)

◆ operator*() [62/76]

Frm_Product<Cmplx,Cmplx,Real> concepts::operator* ( const Formula< Cmplx > &  frm1,
const Formula< Real > &  frm2 
)

◆ operator*() [63/76]

Frm_Product<Cmplx,Real> concepts::operator* ( const Formula< Real > &  frm,
const Cmplx  a 
)

◆ operator*() [64/76]

Frm_Product<Real> concepts::operator* ( const Formula< Real > &  frm,
const Real  a 
)

◆ operator*() [65/76]

Frm_Product<Cmplx,Real> concepts::operator* ( const Formula< Real > &  frm1,
const Formula< Cmplx > &  frm2 
)

◆ operator*() [66/76]

Frm_Product<Real> concepts::operator* ( const Formula< Real > &  frm1,
const Formula< Real > &  frm2 
)

◆ operator*() [67/76]

template<class F , class G >
Array<typename Combtype<F,G>::type> concepts::operator* ( const G &  val,
const Array< F > &  array 
)

Multiplication operator.

Returns the product of an a value of type G and an array of type F.

Definition at line 375 of file array.hh.

◆ operator*() [68/76]

template<uint dim>
Cmplx concepts::operator* ( const Point< Cmplx, dim > &  a,
const Point< Real, dim > &  b 
)

Definition at line 252 of file vectorsMatrices.hh.

◆ operator*() [69/76]

template<uint dim>
Cmplx concepts::operator* ( const Point< Real, dim > &  a,
const Point< Cmplx, dim > &  b 
)

Definition at line 261 of file vectorsMatrices.hh.

◆ operator*() [70/76]

ElementFormulaContainer<MapCmplx2d> concepts::operator* ( const Real  a,
const ElementFormulaContainer< MapCmplx2d >  frm 
)

◆ operator*() [71/76]

ElementFormulaContainer<MapReal2d> concepts::operator* ( const Real  a,
const ElementFormulaContainer< MapReal2d >  frm 
)

◆ operator*() [72/76]

BilinearFormContainer<Cmplx> concepts::operator* ( const Real  w,
const BilinearFormContainer< Cmplx >  frm1 
)

◆ operator*() [73/76]

BilinearFormContainer<Real> concepts::operator* ( const Real  w,
const BilinearFormContainer< Real >  frm1 
)

◆ operator*() [74/76]

template<class F , uint dim>
Point<typename Combtype<F,Real>::type,dim> concepts::operator* ( const Real  x,
const Point< F, dim > &  y 
)
inline

Definition at line 240 of file vectorsMatrices.hh.

◆ operator*() [75/76]

template<class F , class G >
Sequence<typename Combtype<F,G>::type> concepts::operator* ( const Sequence< F >  seq1,
const G  factor 
)

Definition at line 448 of file sequence.hh.

◆ operator*() [76/76]

template<class F , class G >
Sequence<typename Combtype<F,G>::type> concepts::operator* ( const Sequence< F >  seq1,
const Sequence< G >  seq2 
)

Definition at line 434 of file sequence.hh.

◆ operator+() [1/29]

BilinearFormContainer<Cmplx> concepts::operator+ ( const BilinearFormContainer< Cmplx >  frm1,
const BilinearFormContainer< Cmplx >  frm2 
)

◆ operator+() [2/29]

BilinearFormContainer<Cmplx> concepts::operator+ ( const BilinearFormContainer< Cmplx >  frm1,
const BilinearFormContainer< Real >  frm2 
)

◆ operator+() [3/29]

BilinearFormContainer<Cmplx> concepts::operator+ ( const BilinearFormContainer< Real >  frm1,
const BilinearFormContainer< Cmplx >  frm2 
)

◆ operator+() [4/29]

BilinearFormContainer<Real> concepts::operator+ ( const BilinearFormContainer< Real >  frm1,
const BilinearFormContainer< Real >  frm2 
)

Simple adding two element formulas by +-operator.

◆ operator+() [5/29]

ElementFormulaContainer<Cmplx> concepts::operator+ ( const ElementFormulaContainer< Cmplx >  frm,
const Cmplx  a 
)

◆ operator+() [6/29]

ElementFormulaContainer<Cmplx> concepts::operator+ ( const ElementFormulaContainer< Cmplx >  frm,
const Real  a 
)

◆ operator+() [7/29]

ElementFormulaContainer<Cmplx> concepts::operator+ ( const ElementFormulaContainer< Cmplx >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator+() [8/29]

ElementFormulaContainer<Cmplx> concepts::operator+ ( const ElementFormulaContainer< Cmplx >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

◆ operator+() [9/29]

ElementFormulaContainer<Cmplx2d> concepts::operator+ ( const ElementFormulaContainer< Cmplx2d >  frm,
const Cmplx2d  a 
)

◆ operator+() [10/29]

ElementFormulaContainer<Cmplx2d> concepts::operator+ ( const ElementFormulaContainer< Cmplx2d >  frm,
const Real2d  a 
)

◆ operator+() [11/29]

ElementFormulaContainer<Cmplx2d> concepts::operator+ ( const ElementFormulaContainer< Cmplx2d >  frm1,
const ElementFormulaContainer< Cmplx2d >  frm2 
)

◆ operator+() [12/29]

ElementFormulaContainer<Cmplx2d> concepts::operator+ ( const ElementFormulaContainer< Cmplx2d >  frm1,
const ElementFormulaContainer< Real2d >  frm2 
)

◆ operator+() [13/29]

ElementFormulaContainer<Cmplx> concepts::operator+ ( const ElementFormulaContainer< Real >  frm,
const Cmplx  a 
)

◆ operator+() [14/29]

ElementFormulaContainer<Real> concepts::operator+ ( const ElementFormulaContainer< Real >  frm,
const Real  a 
)

Simple adding of a element formulas and a constant via +-operator.

◆ operator+() [15/29]

ElementFormulaContainer<Cmplx> concepts::operator+ ( const ElementFormulaContainer< Real >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator+() [16/29]

ElementFormulaContainer<Real> concepts::operator+ ( const ElementFormulaContainer< Real >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

Simple adding two element formulas by +-operator.

◆ operator+() [17/29]

ElementFormulaContainer<Cmplx2d> concepts::operator+ ( const ElementFormulaContainer< Real2d >  frm,
const Cmplx2d  a 
)

◆ operator+() [18/29]

ElementFormulaContainer<Real2d> concepts::operator+ ( const ElementFormulaContainer< Real2d >  frm,
const Real2d  a 
)

◆ operator+() [19/29]

ElementFormulaContainer<Cmplx2d> concepts::operator+ ( const ElementFormulaContainer< Real2d >  frm1,
const ElementFormulaContainer< Cmplx2d >  frm2 
)

◆ operator+() [20/29]

ElementFormulaContainer<Real2d> concepts::operator+ ( const ElementFormulaContainer< Real2d >  frm1,
const ElementFormulaContainer< Real2d >  frm2 
)

◆ operator+() [21/29]

Frm_Sum<Cmplx> concepts::operator+ ( const Formula< Cmplx > &  frm,
const Cmplx  a 
)

◆ operator+() [22/29]

Frm_Sum<Cmplx,Cmplx,Real> concepts::operator+ ( const Formula< Cmplx > &  frm,
const Real  a 
)

◆ operator+() [23/29]

Frm_Sum<Cmplx> concepts::operator+ ( const Formula< Cmplx > &  frm1,
const Formula< Cmplx > &  frm2 
)

◆ operator+() [24/29]

Frm_Sum<Cmplx,Cmplx,Real> concepts::operator+ ( const Formula< Cmplx > &  frm1,
const Formula< Real > &  frm2 
)

◆ operator+() [25/29]

Frm_Sum<Cmplx,Real> concepts::operator+ ( const Formula< Real > &  frm,
const Cmplx  a 
)

◆ operator+() [26/29]

Frm_Sum<Real> concepts::operator+ ( const Formula< Real > &  frm,
const Real  a 
)

Simple adding two formulas by +-operator. 

concepts::ParsedFormula<> a("(x+y+z)");
concepts::ParsedFormula<> b("(x+y+2*z)");
std::cout << "a+b = " << a+b << std::endl;

◆ operator+() [27/29]

Frm_Sum<Cmplx,Real> concepts::operator+ ( const Formula< Real > &  frm1,
const Formula< Cmplx > &  frm2 
)

◆ operator+() [28/29]

Frm_Sum<Real> concepts::operator+ ( const Formula< Real > &  frm1,
const Formula< Real > &  frm2 
)

◆ operator+() [29/29]

template<class _Tp , class _Ref , class _Ptr >
_Matrix_iterator_base<_Tp, _Ref, _Ptr> concepts::operator+ ( ptrdiff_t  __n,
const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &  __x 
)
inline

Definition at line 249 of file matrixIterator.hh.

◆ operator-() [1/21]

template<typename _Tp , typename _RefL , typename _PtrL , typename _RefR , typename _PtrR >
_Matrix_iterator_base<_Tp, _RefL, _PtrL>::difference_type concepts::operator- ( const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &  __x,
const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &  __y 
)
inline

Definition at line 235 of file matrixIterator.hh.

◆ operator-() [2/21]

BilinearFormContainer<Cmplx> concepts::operator- ( const BilinearFormContainer< Cmplx >  frm1,
const BilinearFormContainer< Cmplx >  frm2 
)

◆ operator-() [3/21]

BilinearFormContainer<Cmplx> concepts::operator- ( const BilinearFormContainer< Cmplx >  frm1,
const BilinearFormContainer< Real >  frm2 
)

◆ operator-() [4/21]

BilinearFormContainer<Cmplx> concepts::operator- ( const BilinearFormContainer< Real >  frm1,
const BilinearFormContainer< Cmplx >  frm2 
)

◆ operator-() [5/21]

BilinearFormContainer<Real> concepts::operator- ( const BilinearFormContainer< Real >  frm1,
const BilinearFormContainer< Real >  frm2 
)

Simple adding two element formulas by +-operator.

◆ operator-() [6/21]

ElementFormulaContainer<Cmplx> concepts::operator- ( const ElementFormulaContainer< Cmplx >  frm,
const Cmplx  a 
)

◆ operator-() [7/21]

ElementFormulaContainer<Cmplx> concepts::operator- ( const ElementFormulaContainer< Cmplx >  frm,
const Real  a 
)

◆ operator-() [8/21]

ElementFormulaContainer<Cmplx> concepts::operator- ( const ElementFormulaContainer< Cmplx >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator-() [9/21]

ElementFormulaContainer<Cmplx> concepts::operator- ( const ElementFormulaContainer< Cmplx >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

◆ operator-() [10/21]

ElementFormulaContainer<Cmplx2d> concepts::operator- ( const ElementFormulaContainer< Cmplx2d >  frm,
const Cmplx2d  a 
)

◆ operator-() [11/21]

ElementFormulaContainer<Cmplx2d> concepts::operator- ( const ElementFormulaContainer< Cmplx2d >  frm,
const Real2d  a 
)

◆ operator-() [12/21]

ElementFormulaContainer<Cmplx2d> concepts::operator- ( const ElementFormulaContainer< Cmplx2d >  frm1,
const ElementFormulaContainer< Cmplx2d >  frm2 
)

◆ operator-() [13/21]

ElementFormulaContainer<Cmplx2d> concepts::operator- ( const ElementFormulaContainer< Cmplx2d >  frm1,
const ElementFormulaContainer< Real2d >  frm2 
)

◆ operator-() [14/21]

ElementFormulaContainer<Cmplx> concepts::operator- ( const ElementFormulaContainer< Real >  frm,
const Cmplx  a 
)

◆ operator-() [15/21]

ElementFormulaContainer<Real> concepts::operator- ( const ElementFormulaContainer< Real >  frm,
const Real  a 
)

Simple subtracting of a element formulas and a constant via –operator.

◆ operator-() [16/21]

ElementFormulaContainer<Cmplx> concepts::operator- ( const ElementFormulaContainer< Real >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator-() [17/21]

ElementFormulaContainer<Real> concepts::operator- ( const ElementFormulaContainer< Real >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

Simple subtracting two element formulas by "-"-operator.

◆ operator-() [18/21]

ElementFormulaContainer<Cmplx2d> concepts::operator- ( const ElementFormulaContainer< Real2d >  frm,
const Cmplx2d  a 
)

◆ operator-() [19/21]

ElementFormulaContainer<Real2d> concepts::operator- ( const ElementFormulaContainer< Real2d >  frm,
const Real2d  a 
)

◆ operator-() [20/21]

ElementFormulaContainer<Cmplx2d> concepts::operator- ( const ElementFormulaContainer< Real2d >  frm1,
const ElementFormulaContainer< Cmplx2d >  frm2 
)

◆ operator-() [21/21]

ElementFormulaContainer<Real2d> concepts::operator- ( const ElementFormulaContainer< Real2d >  frm1,
const ElementFormulaContainer< Real2d >  frm2 
)

◆ operator/() [1/10]

ElementFormulaContainer<Cmplx> concepts::operator/ ( const ElementFormulaContainer< Cmplx >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator/() [2/10]

ElementFormulaContainer<Cmplx> concepts::operator/ ( const ElementFormulaContainer< Cmplx >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

◆ operator/() [3/10]

ElementFormulaContainer<Cmplx2d> concepts::operator/ ( const ElementFormulaContainer< Cmplx2d >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator/() [4/10]

ElementFormulaContainer<Cmplx2d> concepts::operator/ ( const ElementFormulaContainer< Cmplx2d >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

◆ operator/() [5/10]

ElementFormulaContainer<Cmplx> concepts::operator/ ( const ElementFormulaContainer< Real >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator/() [6/10]

ElementFormulaContainer<Real> concepts::operator/ ( const ElementFormulaContainer< Real >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

Division of a element formulas by a scalar element formula via /-operator.

◆ operator/() [7/10]

ElementFormulaContainer<Cmplx2d> concepts::operator/ ( const ElementFormulaContainer< Real2d >  frm1,
const ElementFormulaContainer< Cmplx >  frm2 
)

◆ operator/() [8/10]

ElementFormulaContainer<Real2d> concepts::operator/ ( const ElementFormulaContainer< Real2d >  frm1,
const ElementFormulaContainer< Real >  frm2 
)

Division of a vector valued element formulas by a scalar element formula via /-operator.

◆ operator/() [9/10]

template<class F , class G >
Sequence<typename Combtype<F,G>::type> concepts::operator/ ( const Sequence< F >  seq1,
const G  divisor 
)

Definition at line 475 of file sequence.hh.

◆ operator/() [10/10]

template<class F , class G >
Sequence<typename Combtype<F,G>::type> concepts::operator/ ( const Sequence< F >  seq1,
const Sequence< G >  seq2 
)

Definition at line 461 of file sequence.hh.

◆ operator<() [1/4]

template<class _Tp , class _Ref , class _Ptr >
bool concepts::operator< ( const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &  __x,
const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &  __y 
)
inline

Definition at line 165 of file matrixIterator.hh.

◆ operator<() [2/4]

template<class _Tp , class _RefL , class _PtrL , class _RefR , class _PtrR >
bool concepts::operator< ( const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &  __x,
const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &  __y 
)
inline

Definition at line 175 of file matrixIterator.hh.

◆ operator<() [3/4]

bool concepts::operator< ( const Cell &  cell_x,
const Cell &  cell_y 
)

<-operator could be useful for sorting, e.g. in std::set.

◆ operator<() [4/4]

bool concepts::operator< ( const Connector &  cntr_x,
const Connector &  cntr_y 
)

<-operator sorted by the key, it could be useful for sorting, e.g.

in std::set.

◆ operator<<() [1/28]

template<class F >
::std::ostream& concepts::operator<< ( ::std::ostream &  os,
TColumn< F > *  T 
)

output-operator for pointer to TColumn, gives either 0 or TColumn itself

Definition at line 110 of file tmatrix.hh.

◆ operator<<() [2/28]

template<uint levelDim>
std::ostream& concepts::operator<< ( std::ostream &  os,
const AdaptiveAdjust< levelDim > &  a 
)

◆ operator<<() [3/28]

template<int dim>
std::ostream& concepts::operator<< ( std::ostream &  os,
const AdaptiveAdjustP< dim > &  a 
)

Definition at line 129 of file hpMethod.hh.

◆ operator<<() [4/28]

template<class F >
std::ostream& concepts::operator<< ( std::ostream &  os,
const AdaptiveControl< F > &  c 
)

◆ operator<<() [5/28]

template<int dim, class F >
std::ostream& concepts::operator<< ( std::ostream &  os,
const AdaptiveControlP< dim, F > &  a 
)

Definition at line 44 of file hpMethod.hh.

◆ operator<<() [6/28]

std::ostream& concepts::operator<< ( std::ostream &  os,
const AdaptiveControlTag &  c 
)

◆ operator<<() [7/28]

template<class F >
std::ostream& concepts::operator<< ( std::ostream &  os,
const Array< F > &  o 
)

Definition at line 319 of file array.hh.

◆ operator<<() [8/28]

std::ostream& concepts::operator<< ( std::ostream &  os,
const CellData &  c 
)

◆ operator<<() [9/28]

template<class F >
std::ostream& concepts::operator<< ( std::ostream &  os,
const ElementMatrix< F > &  o 
)

Definition at line 334 of file element.hh.

◆ operator<<() [10/28]

template<class F >
std::ostream& concepts::operator<< ( std::ostream &  os,
const Graph< F > &  Value 
)

Definition at line 115 of file graph.hh.

◆ operator<<() [11/28]

template<class F >
std::ostream& concepts::operator<< ( std::ostream &  os,
const GraphVertex< F > &  Value 
)

Definition at line 68 of file graph.hh.

◆ operator<<() [12/28]

template<typename T >
std::ostream& concepts::operator<< ( std::ostream &  os,
const HashedSparseMatrix< T > &  o 
)

Definition at line 196 of file hashedSMatrix.hh.

◆ operator<<() [13/28]

std::ostream& concepts::operator<< ( std::ostream &  os,
const IndexRange &  i 
)

◆ operator<<() [14/28]

template<class T , unsigned nlnk>
std::ostream & concepts::operator<< ( std::ostream &  os,
const Joiner< T, nlnk > &  j 
)

Definition at line 161 of file scannerConnectors.hh.

◆ operator<<() [15/28]

template<uint dim>
std::ostream& concepts::operator<< ( std::ostream &  os,
const Level< dim > &  c 
)

◆ operator<<() [16/28]

template<class F , uint DimY, uint DimX>
std::ostream& concepts::operator<< ( std::ostream &  os,
const Mapping< F, DimY, DimX > &  m 
)

Definition at line 609 of file vectorsMatrices.hh.

◆ operator<<() [17/28]

template<int number>
std::ostream& concepts::operator<< ( std::ostream &  os,
const Orders< number > &  o 
)

Definition at line 43 of file karniadakis.hh.

◆ operator<<() [18/28]

template<class F , uint dim>
std::ostream& concepts::operator<< ( std::ostream &  os,
const Point< F, dim > &  p 
)

Definition at line 213 of file vectorsMatrices.hh.

◆ operator<<() [19/28]

std::ostream& concepts::operator<< ( std::ostream &  os,
const Quad2d::Index &  i 
)

◆ operator<<() [20/28]

template<class F , class G >
std::ostream& concepts::operator<< ( std::ostream &  os,
const std::map< F, G * > &  m 
)

Definition at line 79 of file outputOperator.hh.

◆ operator<<() [21/28]

template<class F , class G >
std::ostream& concepts::operator<< ( std::ostream &  os,
const std::map< F, G > &  m 
)

Definition at line 90 of file outputOperator.hh.

◆ operator<<() [22/28]

std::ostream& concepts::operator<< ( std::ostream &  os,
const std::map< uint, IndexRange > &  map 
)

◆ operator<<() [23/28]

template<class F , class G >
std::ostream& concepts::operator<< ( std::ostream &  os,
const std::pair< F, G > &  p 
)

Definition at line 72 of file outputOperator.hh.

◆ operator<<() [24/28]

template<class F >
std::ostream& concepts::operator<< ( std::ostream &  os,
const std::unique_ptr< F > &  p 
)

Definition at line 54 of file outputOperator.hh.

◆ operator<<() [25/28]

template<class T >
std::ostream& concepts::operator<< ( std::ostream &  os,
const std::vector< T * > &  field 
)

Definition at line 149 of file meshImport.hh.

◆ operator<<() [26/28]

std::ostream& concepts::operator<< ( std::ostream &  os,
const Triangle2d::Index &  i 
)

◆ operator<<() [27/28]

std::ostream& concepts::operator<< ( std::ostream &  os,
const Triangle3d::Index &  i 
)

◆ operator<<() [28/28]

template<class F >
std::ostream& concepts::operator<< ( std::ostream &  os,
std::unique_ptr< F > &  a 
)

Output operator for unique_ptr's.

Definition at line 32 of file array.hh.

◆ operator<=() [1/2]

template<class _Tp , class _Ref , class _Ptr >
bool concepts::operator<= ( const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &  __x,
const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &  __y 
)
inline

Definition at line 201 of file matrixIterator.hh.

◆ operator<=() [2/2]

template<class _Tp , class _RefL , class _PtrL , class _RefR , class _PtrR >
bool concepts::operator<= ( const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &  __x,
const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &  __y 
)
inline

Definition at line 209 of file matrixIterator.hh.

◆ operator==() [1/6]

template<class _Tp , class _Ref , class _Ptr >
bool concepts::operator== ( const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &  __x,
const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &  __y 
)
inline

Definition at line 130 of file matrixIterator.hh.

◆ operator==() [2/6]

template<class _Tp , class _RefL , class _PtrL , class _RefR , class _PtrR >
bool concepts::operator== ( const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &  __x,
const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &  __y 
)
inline

Definition at line 140 of file matrixIterator.hh.

◆ operator==() [3/6]

template<class F >
bool concepts::operator== ( const Array< F > &  x,
const Array< F > &  y 
)
inline

Definition at line 327 of file array.hh.

◆ operator==() [4/6]

template<class F >
bool concepts::operator== ( const Array< F > &  x,
F &  y 
)
inline

Definition at line 338 of file array.hh.

◆ operator==() [5/6]

template<class F , uint dim>
bool concepts::operator== ( const Point< F, dim > &  x,
const Point< F, dim > &  y 
)
inline

Definition at line 231 of file vectorsMatrices.hh.

◆ operator==() [6/6]

template<class F >
bool concepts::operator== ( F &  y,
const Array< F > &  x 
)
inline

Definition at line 348 of file array.hh.

◆ operator>() [1/2]

template<class _Tp , class _Ref , class _Ptr >
bool concepts::operator> ( const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &  __x,
const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &  __y 
)
inline

Definition at line 186 of file matrixIterator.hh.

◆ operator>() [2/2]

template<class _Tp , class _RefL , class _PtrL , class _RefR , class _PtrR >
bool concepts::operator> ( const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &  __x,
const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &  __y 
)
inline

Definition at line 194 of file matrixIterator.hh.

◆ operator>=() [1/2]

template<class _Tp , class _Ref , class _Ptr >
bool concepts::operator>= ( const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &  __x,
const _Matrix_iterator_base< _Tp, _Ref, _Ptr > &  __y 
)
inline

Definition at line 218 of file matrixIterator.hh.

◆ operator>=() [2/2]

template<class _Tp , class _RefL , class _PtrL , class _RefR , class _PtrR >
bool concepts::operator>= ( const _Matrix_iterator_base< _Tp, _RefL, _PtrL > &  __x,
const _Matrix_iterator_base< _Tp, _RefR, _PtrR > &  __y 
)
inline

Definition at line 226 of file matrixIterator.hh.

◆ operator>>() [1/2]

template<class F >
std::istream& concepts::operator>> ( std::istream &  is,
BaseSequence< F > &  seq 
)

Definition at line 133 of file sequence.hh.

◆ operator>>() [2/2]

template<class F >
std::istream& concepts::operator>> ( std::istream &  is,
BaseSet< F > &  set 
)

Definition at line 134 of file set.hh.

◆ outputMatlab() [1/5]

template<class F >
std::ostream& concepts::outputMatlab ( std::ostream &  os,
const ElementMatrix< F > &  em 
)
inline

Function for output of ElementMatrix to Matlab.

example use: outputMatlab(std::cout << "M = ",M) << std::endl;

Definition at line 88 of file outputMatlab.hh.

◆ outputMatlab() [2/5]

template<typename T >
std::ostream& concepts::outputMatlab ( std::ostream &  os,
const std::complex< T > &  val 
)

Definition at line 36 of file outputMatlab.hh.

◆ outputMatlab() [3/5]

template<typename T >
std::ostream& concepts::outputMatlab ( std::ostream &  os,
const T &  val 
)

Function for output of basic types to matlab.

example use: outputMatlab(std::cout << "x = ",x) << std::endl;

Definition at line 30 of file outputMatlab.hh.

◆ outputMatlab() [4/5]

std::ostream& concepts::outputMatlab ( std::ostream &  os,
const TMatrix< Real > &  T 
)
inline

Function for output of T-Matrix to Matlab.

example use: outputMatlab(std::cout << "T = ",T) << std::endl;

Definition at line 22 of file outputMatlab.hh.

◆ outputMatlab() [5/5]

std::ostream& concepts::outputMatlab ( std::ostream &  os,
const TMatrixBase< Real > &  T 
)
inline

Function for output of T-Matrix base class to Matlab.

example use: outputMatlab(std::cout << "T = ",T) << std::endl;

Definition at line 73 of file outputMatlab.hh.

◆ pointerOutput() [1/4]

template<class F >
void concepts::pointerOutput ( std::ostream &  os,
const Array< F > &  array 
)

Definition at line 387 of file array.hh.

◆ pointerOutput() [2/4]

template<class F >
void concepts::pointerOutput ( std::ostream &  os,
const F &  val 
)

Definition at line 16 of file pointerOutput.hh.

◆ pointerOutput() [3/4]

template<class F >
void concepts::pointerOutput ( std::ostream &  os,
const F *  val 
)

Definition at line 21 of file pointerOutput.hh.

◆ pointerOutput() [4/4]

template<class F >
void concepts::pointerOutput ( std::ostream &  os,
F *  val 
)

Definition at line 27 of file pointerOutput.hh.

◆ prodTranspose() [1/2]

template<class F , uint dim>
Mapping<F,dim> concepts::prodTranspose ( const Mapping< F, dim > &  m)

Definition at line 50 of file operations.hh.

◆ prodTranspose() [2/2]

template<class F , uint dim>
Mapping<F,dim>& concepts::prodTranspose ( Mapping< F, dim > &  m)

Definition at line 46 of file operations.hh.

◆ product() [1/2]

template<class F , class G >
G concepts::product ( const F &  m,
const G &  v 
)

Definition at line 41 of file operations.hh.

◆ product() [2/2]

template<class F , class G >
G& concepts::product ( const F &  m,
G &  v 
)

Definition at line 36 of file operations.hh.

◆ quadratureWeightTensor() [1/2]

Array<Real> concepts::quadratureWeightTensor ( const Array< QuadratureRule1d * > &  ArrayQuad1D)

Computes a multi-dimensional quadrature weight tensor.

Parameters
ArrayQuad1Dpointers to 1D quadratures
Author
Adrien Semin, 2015

◆ quadratureWeightTensor() [2/2]

Real concepts::quadratureWeightTensor ( const Array< QuadratureRule1d * > &  ArrayQuad1D,
const Array< int > &  Index 
)

Compute a quadrature weight tensor at a partical index point.

Parameters
ArrayQuad1Dpointers to 1D quadratures
Indexindex to compute
Author
Adrien Semin, 2015

◆ ReadEigenValuesFromFile()

concepts::Sequence<Cmplx> concepts::ReadEigenValuesFromFile ( const int  NDtN_given,
const std::string  Filename 
)

Definition at line 762 of file DtNmap2D_visc.hh.

◆ realSeqFromStringWithPower()

Sequence<Real> concepts::realSeqFromStringWithPower ( const std::string  s)

Converts a string to a sequence of real numbers, where a power may be allowed to express, e.g., negative powers of 2.

The string "1.0 2e-8 2p-2" results in Sequence(1, 2e-08, 0.25)

◆ removeAllWhite()

std::string concepts::removeAllWhite ( const std::string  str)

Removes all white space in the string str.

◆ securePointer() [1/2]

template<class F , class G >
F* concepts::securePointer ( const F  value,
const G *  matrix 
)

Definition at line 265 of file matrixIterator.hh.

◆ securePointer() [2/2]

template<class F , class G >
F* concepts::securePointer ( F &  value,
G *  matrix 
)

Templated function, which prevent a pointer to a temporary value got from constant matrices with index operator .

Author
Kersten Schmidt, 2005

Definition at line 262 of file matrixIterator.hh.

◆ sgn()

int concepts::sgn ( const Real  d)

Definition at line 37 of file DtNmap2D_visc.hh.

◆ sparseLineToArrays()

template<typename F >
void concepts::sparseLineToArrays ( std::map< int, F > &  line,
F *  a,
int *  asub 
)

This function converts a sparse line to an array of values and an array of indices.

Author
, Kersten Schmidt, 2005

Definition at line 63 of file CRS.hh.

◆ splitString()

std::vector<std::string> concepts::splitString ( const std::string  text,
const std::string  separators 
)

Split the string text string into words, where the separation token are included in separators.

◆ splitStringByComma()

std::vector<std::string> concepts::splitStringByComma ( const std::string  text)

Split a strings in words separated by commas while respecting the bracket hierachies.

It splits "Ellipse(1.0, 4), Circle()" into "Ellipse(1.0, 4)" and "Circle()".

◆ splitStringNameParams()

std::vector<std::string> concepts::splitStringNameParams ( const std::string  text)

Split a string like "Ellipse(1.0, 4)" into "Ellipse", "1.0", "4".

◆ sqr()

Real concepts::sqr ( const Real  x)

Definition at line 27 of file DtNmap2D_visc.hh.

◆ storeDenseMatrixToMatlab() [1/2]

template<class F >
bool concepts::storeDenseMatrixToMatlab ( F &  matrix,
const uint  nofRows,
const uint  nofCols,
const std::string  filename,
std::string  name = "",
bool  append = false 
)

Stores a matrix to the matlab file filename as dense matrix name.

If append is false, overwrite old file, if already existed.

Its applicable for any concepts::Matrix and for concepts::ElementMatrix as well.

Returns
true if the writing to the file was successfull
Author
Kersten Schmidt, 2005

Definition at line 32 of file outputMatlab.hh.

◆ storeDenseMatrixToMatlab() [2/2]

template<class F >
void concepts::storeDenseMatrixToMatlab ( F &  matrix,
const uint  nofRows,
const uint  nofCols,
std::ostream &  ofs,
std::string  name = "" 
)

Writes a matrix to the stream ofs as dense matrix name in Matlab format.

Its applicable for any concepts::Matrix and for concepts::ElementMatrix as well.

Returns
true if the writing to the file was successfull
Author
Kersten Schmidt, 2005

Definition at line 62 of file outputMatlab.hh.

◆ storeSparseMatrixToOctave()

template<class F >
void concepts::storeSparseMatrixToOctave ( SparseMatrix< F > &  matrix,
std::ostream &  ofs,
std::string  name = "" 
)

Writes a matrix to the stream ofs as dense matrix name in Octave format (older version don't have sparse matrix format).

Its applicable for any concepts::Matrix and for concepts::HashedSMatrix as well.

Returns
true if the writing to the file was successfull
Author
Kersten Schmidt, 2005

Definition at line 98 of file outputMatlab.hh.

◆ stringSubs()

template<class F >
std::string concepts::stringSubs ( const std::string  str,
const std::string  var,
F  value 
)

Substitute all occurances of a substring var of a string str by value which may be for example a real or another string.

Definition at line 81 of file stringFunc.hh.

◆ stringtolower()

std::string concepts::stringtolower ( const std::string  s)

◆ tolower()

char concepts::tolower ( const char  ch)

◆ transpose() [1/2]

template<class F , uint dim>
Mapping<F,dim> concepts::transpose ( const Mapping< F, dim > &  m)

Definition at line 58 of file operations.hh.

◆ transpose() [2/2]

template<class F , uint dim>
Mapping<F,dim>& concepts::transpose ( Mapping< F, dim > &  m)

Definition at line 54 of file operations.hh.

◆ typeOf()

template<class T >
std::string concepts::typeOf ( const T &  t)

Return the typeid name of a class object.

Parameters
tObject whose type has to be determined
Author
Robert Gruhlke, Adrien Semin 2016

Definition at line 43 of file output.hh.

◆ uintSeqSets()

Sequence<concepts::Set<uint> > concepts::uintSeqSets ( const std::string  s)

Converts a string to a sequence of sets of uint.

The numbers in each set are separated by a comma, whereas the differents sets are separated by a semicolon.

The string "1, 2, 3; 4" results in Sequence(Set(1,2,3), Set(4))

◆ visc_ell_fast()

Cmplx concepts::visc_ell_fast ( const Cmplx  lambda,
const Real  nu,
const Real  omega,
const Real  rho0 
)

Definition at line 44 of file DtNmap2D_visc.hh.

◆ visc_ell_slow()

Cmplx concepts::visc_ell_slow ( const Cmplx  lambda,
const Real  nu,
const Real  omega,
const Real  rho0,
const Real  c0 
)

Definition at line 63 of file DtNmap2D_visc.hh.

Variable Documentation

◆ storeDenseMatrixMatlabCounter_

uint concepts::storeDenseMatrixMatlabCounter_ = 0
static

Counts number of Matlab outputs (used to uniquely name the matrices)

Definition at line 17 of file outputMatlab.hh.

◆ storeSparseMatrixMatlabCounter_

uint concepts::storeSparseMatrixMatlabCounter_ = 0
static

Definition at line 18 of file outputMatlab.hh.

Page URL: http://wiki.math.ethz.ch/bin/view/Concepts/WebHome
21 August 2020
© 2020 Eidgenössische Technische Hochschule Zürich