Home | Doxygen Documentation | Tutorials | Developer Tools (restricted)
hpFEM2d.cc

Introduction

Two dimensional FEM in Concepts. This code features high order Ansatz functions and irregular meshes (local, anisotropic refinements in h and p). All classes for the hp-FEM in two dimensions can be found in the namespace hp2D.

The equation solved is a reaction-diffusion equation (without reaction term)

\[ - \Delta u = 0 \]

on the L shaped domain (-1,1)2 \ (0,1)x(-1,0) with mixed boundary conditions chosen such that the exact solution is 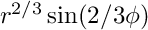$ r^{2/3}\sin(2/3 \phi)$. The linear system is solved using CG or a direct solver.

Lshaped-quad.gif

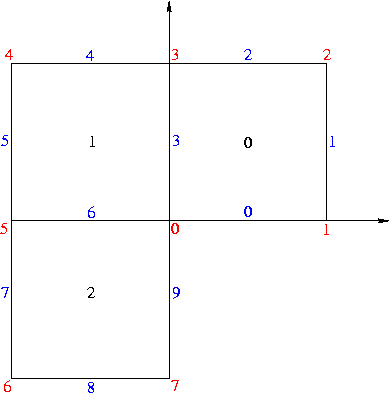The boundary conditions are homogeneous Dirichlet on the edges 0 and 9 and non-zero Neumann on the rest of the boundary.

The exact solution is 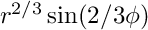$ r^{2/3}\sin(2/3 \phi)$.

The convergence in energy norm is shown in the results section together with plots of the solution.

Contents

  1. Commented Program
    1. FEM Routine
    2. Main Program
  2. Results
  3. Complete Source Code

Commented Program

System include files. 

#include <memory>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <fstream>
#include <iostream>
#include <sstream>
#include <unistd.h>
Concepts include files. hp2D.hh is for the high order method. 
#include "basics.hh"
#include "toolbox.hh"
#include "formula.hh"
#include "geometry.hh"
#include "space.hh"
#include "function.hh"
#include "graphics.hh"
#include "operator.hh"

#include "hp2D.hh"
With this using directive, we do not need to prepend concepts:: before Real everytime. 
using concepts::Real;

FEM Routine

The only parameters of the routine fem are some input parameters in input, the boundary conditions in bc and the additional argument output is used to for the gathering the output. 

void fem(const concepts::InOutParameters& input,
         concepts::BoundaryConditions& bc,
         concepts::InOutParameters& output)
Set up some abbreviations for some parameters found in input. If any of those parameters does not exist in input, an exception is thrown.

l is the number of levels to compute on and p the initial polynomial degree. 

{
  const uint l = input.getInt("level");
  const uint p = input.getInt("polynomial");
meshNameBase contains the base name of the mesh files. 
  const std::string meshNameBase = input.getString("meshNameBase");
exenergy gets the value of the exact energy. 
  const Real exenergy = input.getDouble("exenergy");
solverType holds the type of solver to use:

  const uint solverType = input.getInt("solver");

Mesh

The following lines put together the names for the files which contain the coordinates, the elements and the boundary conditions of the mesh. 

  std::stringstream fileCoord;
  fileCoord << meshNameBase << "Coord.dat" << std::ends;
  output.addString("coordFile", fileCoord.str().c_str());
  std::stringstream fileElements;
  fileElements << meshNameBase << "Elements.dat" << std::ends;
  output.addString("elementsFile", fileElements.str().c_str());
  std::stringstream fileBoundary;
  fileBoundary << meshNameBase << "Boundary.dat" << std::ends;
  output.addString("boundaryFile", fileBoundary.str().c_str());
Then, these names are given to the mesh importer which reads the files and creates a mesh from it. 
  concepts::Import2dMesh msh(fileCoord.str(), fileElements.str(),
                             fileBoundary.str());
  std::cout << "msh = " << msh << std::endl;

Space

Using the mesh, the space can be built. Note that the elements are not yet created as this is an adaptive space. It builds its elements only on request via hp2D::Space::rebuild() 

  hp2D::Space space(msh, 0, p, &bc);
Now, the loop over the different computational levels is initialized. 
  for (uint i = 0; i < l; ++i) {
    std::cout << "i = " << i << std::endl;
timer is used to clock some parts of the code. 
    concepts::ResourceMonitor timer;
Now, it is time to build the elements of the space. If there are degrees of freedom in the space, it might be worth to compute something. Otherwise, we skip directly to the refinement of the space. 
    space.rebuild();
    if (space.dim() > 0) {
The time to build the space and the number of degrees of freedom are stored to generate some statistics in the post-processing. 
      output.addArrayDouble("space_time", i, timer.utime());
      output.addArrayInt("dof", i, space.dim());
The newly built space is printed and written to file in different formats. 
      std::cout << "  space = " << space << std::endl;
      graphics::drawMeshEPS(space, "mesh.eps");
      graphics::drawMeshDX(space, "mesh.dx");

Computations

The right hand side is computed. In our case, the vector rhs only contains the integrals of the Neumann boundary conditions as the right hand side f is 0. 

      hp2D::Riesz<> lform(concepts::ParsedFormula<>
                        (input.getString("f").c_str()), &bc);
      concepts::Vector<Real> rhs(space, lform);

The stiffness matrix is computed from a linear combination of the two bilinear forms hp2D::Laplace and hp2D::Identity. In our case, c is 0 and there is no contribution of hp2D::Identity. Instead of using concepts::BilinearFormLiCo, one could also build a linear combination of the matrices using concepts::LiCo. Sometimes, it is a matter of taste, sometimes a matter of efficiency which one is used. 

      // ** matrices **
      hp2D::Laplace<> la;
      
      // declare formulas for each entry of the 2x2 coefficient matrix
      concepts::ParsedFormula<Real> a11("(x)");
      concepts::ParsedFormula<Real> a12("(1)");
      concepts::ParsedFormula<Real> a21("(1)");
      concepts::ParsedFormula<Real> a22("(1)");

      // assemble the formulas in a MatrixElementFormula
      std::vector< concepts::ElementFormulaContainer<Real> > formulas;
      formulas.push_back(a11);
      formulas.push_back(a21);
      formulas.push_back(a12);
      formulas.push_back(a22);

      concepts::MatrixElementFormula<Real, 2> A(formulas);

      // create the Laplacian-BF with Matrix coefficients
      hp2D::LaplaceMatrix<> lamat( A );

      hp2D::Identity<> id;
#if 0
      concepts::BilinearFormLiCo<Real> bform(la, id, input.getDouble("a"),
                                             input.getDouble("c"));
#else
      concepts::BilinearFormLiCo<Real> bform(lamat, id, input.getDouble("a"),
                                             input.getDouble("c"));
#endif

      concepts::SparseMatrix<Real> la_M(space, la);
      concepts::SparseMatrix<Real> lamat_M(space, lamat);

#if 0
      cout << "la_M: " << concepts::DenseMatrix<Real>( la_M ) << endl;
      cout << "lamat_M: " << concepts::DenseMatrix<Real>( lamat_M ) << endl;
      lamat_M.addInto(la_M, -1);
      cout << "error: " << concepts::DenseMatrix<Real>( la_M ) << endl;
      cout << "error: " <<  la_M << endl;
#endif

      timer.utime();
      concepts::SparseMatrix<Real> stiff(space, bform);
      output.addArrayDouble("stiff_time", i, timer.utime());
      stiff.compress();
      std::cout << "  matrix: " << stiff << std::endl;

The next part is the linear solver. There are quite a few available for Concepts and here is a switch case statement offering a choice among the different solvers (if they are installed -- hence the #ifdef statements). The variable solver makes use of the common base class concepts::Operator of all solvers: it is a pointer to the solver to be chosen in the switch clause. 

      // ** set up solver **
      std::auto_ptr<concepts::Operator<Real> > solver(0);
      std::auto_ptr<concepts::DiagonalMatrix<Real> > diag(0);
      std::auto_ptr<concepts::DiagonalSolver<Real> > precond(0);
#ifdef HAS_PETSC
      std::auto_ptr<concepts::PETScMat> stiffP(0);
#endif
      switch(solverType) {
      case 0:
        diag.reset(new concepts::DiagonalMatrix<Real>(stiff));
        precond.reset(new concepts::DiagonalSolver<Real>(*diag));
        solver.reset(new concepts::CG<Real>(stiff, *precond, 1e-6,
                                            2*stiff.dimX()+100));
        break;
#ifdef HAS_PETSC
      case 1:
        stiffP.reset(new concepts::PETScMat(stiff));
        solver.reset(new concepts::PETSc(*stiffP, 1e-12, "bcgs", "ilu"));
        break;
#endif
#ifdef HAS_SuperLU
      case 2: solver.reset(new concepts::SuperLU<Real>(stiff)); break;
#endif
#ifdef HAS_UMFPACK
      case 3: solver.reset(new concepts::Umfpack(stiff, true)); break;
#endif
#ifdef HAS_PARDISO
      case 4: solver.reset
          (new concepts::Pardiso(stiff, concepts::Pardiso::SYMM_INDEF));
        break;
#endif
      default:
        throw conceptsException
          (concepts::MissingFeature("solver not present"));
      }
Now, everything is prepared to solve the linear system.

sol is an empty vector to hold the solution of the linear system. 

      // ** solve **
      concepts::Vector<Real> sol(space);
      timer.utime();
      (*solver)(rhs, sol);
      output.addArrayDouble("solve_time", i, timer.utime());
Some immediate statistics of the solver. 
      std::cout << "  solver = " << *solver << std::endl;
      std::cout << "  solve time " << output.getArrayDouble("solve_time", i)
                << std::endl;
      switch(solverType) {
      case 0: {
        const concepts::CG<Real>* s =
          dynamic_cast<const concepts::CG<Real>*>(solver.get());
        conceptsAssert(s, concepts::Assertion());
        output.addArrayInt("iterations", i, s->iterations());
        break;
      }
#ifdef HAS_PETSC
      case 1: {
        const concepts::PETSc* s =
          dynamic_cast<const concepts::PETSc*>(solver.get());
        conceptsAssert(s, concepts::Assertion());
        output.addArrayInt("iterations", i, s->iterations());
        break;
      }
#endif
      }

Postprocessing

The energy of the FE solution in sol can be computed by multiplying sol and rhs. It is stored together with the relative error of the FE energy. 

      const Real FEenergy = sol*rhs;
      std::cout << "  FE energy = " << std::setprecision(20)
                << FEenergy << std::setprecision(6);
      output.addArrayDouble("feenergy", i, FEenergy);
      const Real relError = fabs(FEenergy - exenergy)/exenergy;
      std::cout << ", rel. energy error = " << std::setprecision(20)
                << relError << std::setprecision(6) << std::endl;
      output.addArrayDouble("energyError", i, relError);

If it was selected to have graphical representation of the solution, the data is written to a file using graphics::drawDataGnuplot. 

      if (input.getBool("graphics")) {
        std::stringstream name;
        name << "hpFEM2d-" << i << ".gnuplot" << std::ends;
        graphics::drawDataGnuplot(space, name.str(), sol);
      }
    } // if dim > 0

Refinement of the Space

If there are further computations (ie. i < l-1), the space is refined using hp2D::APrioriRefinement towards the vertex (and/or edge) carying a singularity. This information has to be given a-priori by the user. 

    if (i < l-1) {
      int pMax[2] = { 1, 1 };
      hp2D::APrioriRefinement refineSpace(space, input.getInt("vtxRef"),
                                          input.getInt("edgRef"), pMax);
      concepts::GlobalPostprocess<Real> post(space);
      post(refineSpace);
    }
  } // for level i
}

Main Program

Set up the input parameter space (more in the inputoutput.cc tutorial). 

int main(int argc, char** argv) {

  try {
    concepts::InputParser inputParser(true);
Parse the input file and extract the variables from it. Mainly the boundary conditions of the problem are relevant from the input file. 
    concepts::InOutParameters& input = inputParser.inputParameters();
    inputParser.parse(SOURCEDIR "/applications/hpFEM2d.concepts");
Default values for some parameters:

Prepare space for output data (mainly statistics): 

    concepts::InOutParameters& output = inputParser.outputParameters();
    output.addString("version", "$Id: hpFEM2d.cc,v 1.7 2005/03/11 21:34:02 kersten Exp $");

These data should be printed in tabular form at the end of the program: each array which should be included in the table has to be added to table. 

    concepts::ResultsTable table;
    table.addMap(concepts::ResultsTable::INT, "dof", output);
    table.addMap(concepts::ResultsTable::DOUBLE, "energyError", output);
    table.addMap(concepts::ResultsTable::DOUBLE, "feenergy", output);
    table.addMap(concepts::ResultsTable::INT, "iterations", output);
    table.addMap(concepts::ResultsTable::DOUBLE, "space_time", output);
    table.addMap(concepts::ResultsTable::DOUBLE, "stiff_time", output);
    table.addMap(concepts::ResultsTable::DOUBLE, "solve_time", output);

Command Line Arguments

This parses the command line and adds the parameters to input. How this is done is explained in the inputoutput.cc tutorial. 

    // ********************************************************** input data **
    std::string inputfile;
    int opt;
    while ((opt = getopt(argc, argv, "-f:l:p:g")) != EOF)
      switch(opt) {
      case 'l': input.addInt("level", std::atoi(optarg)); break;
      case 'p': input.addInt("polynomial", std::atoi(optarg)); break;
      case 'f': inputfile = std::string(optarg);
        inputParser.parse(inputfile);
        break;
      case 'g': input.addBool("graphics", true); break;
      default:
        std::cout << "Usage: " << argv[0] 
                  << " [-f FILE] [-l LEVEL] [-p DEGREE] [-d]"
                  << std::endl
                  << "where" << std::endl
                  << "  FILE: name of the input file" << std::endl
                  << "  LEVEL: level of refinement" << std::endl
                  << "  DEGREE: polynomial degree" << std::endl
                  << "  -g: graphics of solution" << std::endl
                  << "Options given after the input file override the values "
                  << "read from the"
                  << std::endl << "input file." << std::endl;
        std::exit(1);
        break;
      }
The boundary conditions are read from the input file into input and have to be converted to concepts::BoundaryConditions. The input file contains two arrays: bctype and bcform with the type of the boundary condition and its formula respectively. There are numberbc entries in both arrays and from this data, a concepts::Boundary is constructed and added to bc. 
    // ************************************************* boundary conditions **
    concepts::BoundaryConditions bc;
    for (int i = 1; i <= input.getInt("numberbc"); ++i) {
      bc.add(concepts::Attribute(i),
             concepts::Boundary((concepts::Boundary::boundaryTypes)
                                input.getArrayInt("bctype", i),
                                concepts::ParsedFormula<>
                                (input.getArrayString("bcform", i).c_str())));
    }
The parameters and boundary condition are printed to screen. 
    // ***************************************************** show parameters **
    std::cout << '[' << argv[0] << "]" << std::endl;
    std::cout << "--" << std::endl;
    std::cout << "Parameters:" << std::endl
              << "  input file = " << inputfile << std::endl
              << input;
    std::cout << "--" << std::endl;
    std::cout << bc << std::endl;
    std::cout << "--" << std::endl;

Now, everything is ready to do the computations. 

    // ******************************************************** computations **
    fem(input, bc, output);

The input and output data is stored in a file. The table of output data is printed to screen and stored in a file. 

    // ************************************** output of input data and other **
    std::ofstream* ofs = new std::ofstream(input.getString("gnuplot").c_str());
    *ofs << std::setprecision(20);
    table.print<concepts::ResultsTable::GNUPLOT>(*ofs);
    delete ofs;

    std::cout << "--" << std::endl;
    std::cout << output << std::endl;
    std::cout << table << std::endl;
    std::cout << "--" << std::endl
              << "Writing gathered data to disk: " 
              << input.getString("parameterout") << std::endl;

    ofs = new std::ofstream(input.getString("parameterout").c_str());
    *ofs << "/* program:\t" << argv[0] << std::endl
         << " * command:\t";
    for (int i = 0; i < argc; ++i)
      *ofs << argv[i] << " ";
    *ofs << std::endl
         << " * input file:\t" << inputfile << std::endl;
    *ofs << " */" << std::endl << std::setprecision(20) << inputParser;
    delete ofs;
  }

Finally, exceptions are caught and a sane return value is given back. 

  catch (concepts::ExceptionBase& e) {
    std::cout << e << std::endl;
    return 1;
  }

Results

The input file: 

double  a   1.0
double  c   0.0
string  f   "(0)"

// overkill solution with 6698
double  exenergy  1.8362264461350097

string  meshNameBase  "lshape2D"
int vtxRef    10
int edgRef    0

int numberbc  8
array int   bctype {
  1   1
  2   2
  3   2
  4   2
  5   2
  6   2
  7   2
  8   1
}
array string    bcform {
  1   "(0)"
  2   "( (1/(1+y*y)^(2/3)) * (sin(2/3*atan(y)) - y*cos(2/3*atan(y)))*2/3 )"
  3   "( 2/3/((1+x*x)^(2/3)) * (sin(2/3*atan(1/x)) + x*cos(2/3*atan(1/x))) )"
  4   "( 2/3/((1+x*x)^(2/3)) * (sin(2/3*(atan(1/x)+pi)) + x*cos(2/3*(atan(1/x)+pi))) )"
  5   "( 2/3/((1+y*y)^(2/3)) * (sin(2/3*(atan(-y)+pi)) + y*cos(2/3*(atan(-y)+pi))) )"
  6   "( 2/3/((1+y*y)^(2/3)) * (sin(2/3*(atan(-y)+pi)) + y*cos(2/3*(atan(-y)+pi))) )"
  7   "( 2/3/((1+x*x)^(2/3)) * (sin(2/3*(atan(-1/x)+pi)) - x*cos(2/3*(atan(-1/x)+pi))) )"
  8   "(0)"
}

Output of the program: 

[hpFEM2d]
--
Parameters:
  input file = 
string  author  "(empty)"
string  comment "(empty)"
string  f "(0)"
string  gnuplot "hpFEM2d.gnuplot"
string  meshNameBase  "../../../applications/lshape2D"
string  parameterout  "hpFEM2d.out"
string  title "singularity in (0,0) in L shaped domain"
int edgRef  0
int level 3
int numberbc  8
int polynomial  1
int solver  1
int vtxRef  10
bool  graphics  false
double  a 1
double  c 0
double  exenergy  1.83623
array string bcform {
  1 "(0)"
  2 "( (1/(1+y*y)^(2/3)) * (sin(2/3*atan(y)) - y*cos(2/3*atan(y)))*2/3 )"
  3 "( 2/3/((1+x*x)^(2/3)) * (sin(2/3*atan(1/x)) + x*cos(2/3*atan(1/x))) )"
  4 "( 2/3/((1+x*x)^(2/3)) * (sin(2/3*(atan(1/x)+pi)) + x*cos(2/3*(atan(1/x)+pi))) )"
  5 "( 2/3/((1+y*y)^(2/3)) * (sin(2/3*(atan(-y)+pi)) + y*cos(2/3*(atan(-y)+pi))) )"
  6 "( 2/3/((1+y*y)^(2/3)) * (sin(2/3*(atan(-y)+pi)) + y*cos(2/3*(atan(-y)+pi))) )"
  7 "( 2/3/((1+x*x)^(2/3)) * (sin(2/3*(atan(-1/x)+pi)) - x*cos(2/3*(atan(-1/x)+pi))) )"
  8 "(0)"
}
array int bctype {
  1 1
  2 2
  3 2
  4 2
  5 2
  6 2
  7 2
  8 1
}
--
BoundaryConditions(1: Boundary(DIRICHLET, ParsedFormula(0)), 2: Boundary(NEUMANN, ParsedFormula( (1/(1+y*y)^(2/3)) * (sin(2/3*atan(y)) - y*cos(2/3*atan(y)))*2/3 )), 3: Boundary(NEUMANN, ParsedFormula( 2/3/((1+x*x)^(2/3)) * (sin(2/3*atan(1/x)) + x*cos(2/3*atan(1/x))) )), 4: Boundary(NEUMANN, ParsedFormula( 2/3/((1+x*x)^(2/3)) * (sin(2/3*(atan(1/x)+pi)) + x*cos(2/3*(atan(1/x)+pi))) )), 5: Boundary(NEUMANN, ParsedFormula( 2/3/((1+y*y)^(2/3)) * (sin(2/3*(atan(-y)+pi)) + y*cos(2/3*(atan(-y)+pi))) )), 6: Boundary(NEUMANN, ParsedFormula( 2/3/((1+y*y)^(2/3)) * (sin(2/3*(atan(-y)+pi)) + y*cos(2/3*(atan(-y)+pi))) )), 7: Boundary(NEUMANN, ParsedFormula( 2/3/((1+x*x)^(2/3)) * (sin(2/3*(atan(-1/x)+pi)) - x*cos(2/3*(atan(-1/x)+pi))) )), 8: Boundary(DIRICHLET, ParsedFormula(0)), 0: Boundary(FREE, (0)))
--
msh = Import2dMesh(ncell = 3)
i = 0
  space = Space(dim = 5, nelm = 3)
  matrix: SparseMatrix(5x5, HashedSparseMatrix: 15 (60%) entries bound.)
  solver = PETSc(solves PETScMat(5x5), it = 1, ksp = bcgs, pc = ilu)
  solve time 0
  FE energy = 1.7449022359071539867, rel. energy error = 0.049734721128801930023
i = 1
  space = Space(dim = 16, nelm = 12)
  matrix: SparseMatrix(16x16, HashedSparseMatrix: 90 (35.1562%) entries bound.)
  solver = PETSc(solves PETScMat(16x16), it = 6, ksp = bcgs, pc = ilu)
  solve time 0
  FE energy = 1.7933874905547884104, rel. energy error = 0.023329887046551971153
i = 2
  space = Space(dim = 50, nelm = 21)
  matrix: SparseMatrix(50x50, HashedSparseMatrix: 402 (16.08%) entries bound.)
  solver = PETSc(solves PETScMat(50x50), it = 11, ksp = bcgs, pc = ilu)
  solve time 0
  FE energy = 1.817608097337950035, rel. energy error = 0.010139462284866132546
--
string  boundaryFile  "../../../applications/lshape2DBoundary.dat"
string  coordFile "../../../applications/lshape2DCoord.dat"
string  elementsFile  "../../../applications/lshape2DElements.dat"
array double energyError {
  0 0.0497347
  1 0.0233299
  2 0.0101395
}
array double feenergy {
  0 1.7449
  1 1.79339
  2 1.81761
}
array double solve_time {
  0 0
  1 0
  2 0
}
array double space_time {
  0 0
  1 0.014998
  2 0.043994
}
array double stiff_time {
  0 0
  1 0
  2 0
}
array int dof {
  0 5
  1 16
  2 50
}
array int iterations {
  0 1
  1 6
  2 11
}

ResultsTable(
dof energyError feenergy  solve_time  space_time  stiff_time  dof iterations
0 0.0497347 1.7449  0 0 0 5 1
1 0.0233299 1.79339 0 0.014998  0 16  6
2 0.0101395 1.81761 0 0.043994  0 50  11
)
--
Writing gathered data to disk: hpFEM2d.out

The plot of the solution is done with the following Gnuplot script: 

set style data lines
set ylabel 'y'
set xlabel 'x'
set nokey

set terminal png
set output 'hpFEM2d-solution.png'
splot 'hpFEM2d-2.gnuplot'
hpFEM2d-solution.png

The plot of the solution clearly shows the different elements. They are not connected as concepts::QuadratureRuleGaussJacobi is used for the numerical integration. This rule does not have any points on the boundary of the element. One can also see that there are p + 2 integration points used in each direction per element. In the terminal and first layers, p = 1 and the rest of the layers (only one in this plot) have p = mk in layer k for the linear degree distribution parameter m = 1. Therefore, the elements in the second layer show 4 quadrature points in each direction in the plot.

The plot of the convergence history of the relative energy error is done with the following Gnuplot script: 

set style data linespoints
set logscale y
set ylabel 'relativ energy error'
set xlabel 'ndof'
set format x '%g^3'
set nokey

set grid
set grid mytics

set terminal png
set output 'hpFEM2d-conv.png'
plot 'hpFEM2d.gnuplot' using ($7**(1./3.)):2
hpFEM2d-conv.png

The plot in $\log-\sqrt[3]{.}$ scale shows that the relativ energy error behaves like $\|e\| \leq c \exp(-b N^{1/3})$, where N is the number of degrees of freedom (ndof).

Complete Source Code

Author:
Philipp Frauenfelder, 2004
#include <memory>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <fstream>
#include <iostream>
#include <sstream>
#include <unistd.h>

#include "basics.hh"
#include "toolbox.hh"
#include "formula.hh"
#include "geometry.hh"
#include "space.hh"
#include "function.hh"
#include "graphics.hh"
#include "operator.hh"

#include "hp2D.hh"

using concepts::Real;

// ************************************************************* fem routine **

void fem(const concepts::InOutParameters& input,
         concepts::BoundaryConditions& bc,
         concepts::InOutParameters& output) 
{
  const uint l = input.getInt("level");
  const uint p = input.getInt("polynomial");
  const std::string meshNameBase = input.getString("meshNameBase");
  const Real exenergy = input.getDouble("exenergy");
  const uint solverType = input.getInt("solver");

  std::stringstream fileCoord;
  fileCoord << meshNameBase << "Coord.dat" << std::ends;
  output.addString("coordFile", fileCoord.str().c_str());
  std::stringstream fileElements;
  fileElements << meshNameBase << "Elements.dat" << std::ends;
  output.addString("elementsFile", fileElements.str().c_str());
  std::stringstream fileBoundary;
  fileBoundary << meshNameBase << "Boundary.dat" << std::ends;
  output.addString("boundaryFile", fileBoundary.str().c_str());
  concepts::Import2dMesh msh(fileCoord.str(), fileElements.str(),
                             fileBoundary.str());
  std::cout << "msh = " << msh << std::endl;

  hp2D::Space space(msh, 0, p, &bc);
  for (uint i = 0; i < l; ++i) {
    std::cout << "i = " << i << std::endl;
    concepts::ResourceMonitor timer;
    space.rebuild();
    if (space.dim() > 0) {
      output.addArrayDouble("space_time", i, timer.utime());
      output.addArrayInt("dof", i, space.dim());
      std::cout << "  space = " << space << std::endl;
      graphics::drawMeshEPS(space, "mesh.eps");
      graphics::drawMeshDX(space, "mesh.dx");

      // ** right hand side **
      hp2D::Riesz<> lform(concepts::ParsedFormula<>
                        (input.getString("f").c_str()), &bc);
      concepts::Vector<Real> rhs(space, lform);

      // ** matrices **
      hp2D::Laplace<> la;
      
      // declare formulas for each entry of the 2x2 coefficient matrix
      concepts::ParsedFormula<Real> a11("(x)");
      concepts::ParsedFormula<Real> a12("(1)");
      concepts::ParsedFormula<Real> a21("(1)");
      concepts::ParsedFormula<Real> a22("(1)");

      // assemble the formulas in a MatrixElementFormula
      std::vector< concepts::ElementFormulaContainer<Real> > formulas;
      formulas.push_back(a11);
      formulas.push_back(a21);
      formulas.push_back(a12);
      formulas.push_back(a22);

      concepts::MatrixElementFormula<Real, 2> A(formulas);

      // create the Laplacian-BF with Matrix coefficients
      hp2D::LaplaceMatrix<> lamat( A );

      hp2D::Identity<> id;
#if 0
      concepts::BilinearFormLiCo<Real> bform(la, id, input.getDouble("a"),
                                             input.getDouble("c"));
#else
      concepts::BilinearFormLiCo<Real> bform(lamat, id, input.getDouble("a"),
                                             input.getDouble("c"));
#endif

      concepts::SparseMatrix<Real> la_M(space, la);
      concepts::SparseMatrix<Real> lamat_M(space, lamat);

#if 0
      cout << "la_M: " << concepts::DenseMatrix<Real>( la_M ) << endl;
      cout << "lamat_M: " << concepts::DenseMatrix<Real>( lamat_M ) << endl;
      lamat_M.addInto(la_M, -1);
      cout << "error: " << concepts::DenseMatrix<Real>( la_M ) << endl;
      cout << "error: " <<  la_M << endl;
#endif

      timer.utime();
      concepts::SparseMatrix<Real> stiff(space, bform);
      output.addArrayDouble("stiff_time", i, timer.utime());
      stiff.compress();
      std::cout << "  matrix: " << stiff << std::endl;

      // ** set up solver **
      std::auto_ptr<concepts::Operator<Real> > solver(0);
      std::auto_ptr<concepts::DiagonalMatrix<Real> > diag(0);
      std::auto_ptr<concepts::DiagonalSolver<Real> > precond(0);
#ifdef HAS_PETSC
      std::auto_ptr<concepts::PETScMat> stiffP(0);
#endif
      switch(solverType) {
      case 0:
        diag.reset(new concepts::DiagonalMatrix<Real>(stiff));
        precond.reset(new concepts::DiagonalSolver<Real>(*diag));
        solver.reset(new concepts::CG<Real>(stiff, *precond, 1e-6,
                                            2*stiff.dimX()+100));
        break;
#ifdef HAS_PETSC
      case 1:
        stiffP.reset(new concepts::PETScMat(stiff));
        solver.reset(new concepts::PETSc(*stiffP, 1e-12, "bcgs", "ilu"));
        break;
#endif
#ifdef HAS_SuperLU
      case 2: solver.reset(new concepts::SuperLU<Real>(stiff)); break;
#endif
#ifdef HAS_UMFPACK
      case 3: solver.reset(new concepts::Umfpack(stiff, true)); break;
#endif
#ifdef HAS_PARDISO
      case 4: solver.reset
          (new concepts::Pardiso(stiff, concepts::Pardiso::SYMM_INDEF));
        break;
#endif
      default:
        throw conceptsException
          (concepts::MissingFeature("solver not present"));
      }

      // ** solve **
      concepts::Vector<Real> sol(space);
      timer.utime();
      (*solver)(rhs, sol);
      output.addArrayDouble("solve_time", i, timer.utime());

      std::cout << "  solver = " << *solver << std::endl;
      std::cout << "  solve time " << output.getArrayDouble("solve_time", i)
                << std::endl;
      switch(solverType) {
      case 0: {
        const concepts::CG<Real>* s =
          dynamic_cast<const concepts::CG<Real>*>(solver.get());
        conceptsAssert(s, concepts::Assertion());
        output.addArrayInt("iterations", i, s->iterations());
        break;
      }
#ifdef HAS_PETSC
      case 1: {
        const concepts::PETSc* s =
          dynamic_cast<const concepts::PETSc*>(solver.get());
        conceptsAssert(s, concepts::Assertion());
        output.addArrayInt("iterations", i, s->iterations());
        break;
      }
#endif
      }

      const Real FEenergy = sol*rhs;
      std::cout << "  FE energy = " << std::setprecision(20)
                << FEenergy << std::setprecision(6);
      output.addArrayDouble("feenergy", i, FEenergy);
      const Real relError = fabs(FEenergy - exenergy)/exenergy;
      std::cout << ", rel. energy error = " << std::setprecision(20)
                << relError << std::setprecision(6) << std::endl;
      output.addArrayDouble("energyError", i, relError);

      if (input.getBool("graphics")) {
        std::stringstream name;
        name << "hpFEM2d-" << i << ".gnuplot" << std::ends;
        graphics::drawDataGnuplot(space, name.str(), sol);
      }
    } // if dim > 0

    // ** refinement **
    if (i < l-1) {
      int pMax[2] = { 1, 1 };
      hp2D::APrioriRefinement refineSpace(space, input.getInt("vtxRef"),
                                          input.getInt("edgRef"), pMax);
      concepts::GlobalPostprocess<Real> post(space);
      post(refineSpace);
    }
  } // for level i
}

// ************************************************************ Main Program **

int main(int argc, char** argv) {

  try {
    concepts::InputParser inputParser(true);
    concepts::InOutParameters& input = inputParser.inputParameters();
    inputParser.parse(SOURCEDIR "/applications/hpFEM2d.concepts");

    input.addInt("level", 3);
    input.addInt("polynomial", 1);
    input.addBool("graphics", false);

    input.addDouble("a", 1);
    input.addDouble("c", 0);
    input.addString("f", "(0)");
    input.addInt("vtxRef", 10);
    input.addInt("edgRef", 0);

    input.addInt("solver", 0);

    input.addString("meshNameBase", SOURCEDIR "/applications/lshape2D");

    input.addString("title" , "singularity in (0,0) in L shaped domain");

    std::stringstream outfile;
    outfile << argv[0] << ".out" << std::ends;
    input.addString("parameterout", outfile.str().c_str());

    std::stringstream outfileG;
    outfileG << argv[0] << ".gnuplot" << std::ends;
    input.addString("gnuplot", outfileG.str().c_str());

    concepts::InOutParameters& output = inputParser.outputParameters();
    output.addString("version", "$Id: hpFEM2d.cc,v 1.7 2005/03/11 21:34:02 kersten Exp $");
    output.addArrayDouble("energyError");
    output.addArrayDouble("feenergy");
    output.addArrayInt("dof");
    output.addArrayInt("iterations");
    output.addArrayDouble("space_time");
    output.addArrayDouble("stiff_time");
    output.addArrayDouble("solve_time");
    concepts::ResultsTable table;
    table.addMap(concepts::ResultsTable::INT, "dof", output);
    table.addMap(concepts::ResultsTable::DOUBLE, "energyError", output);
    table.addMap(concepts::ResultsTable::DOUBLE, "feenergy", output);
    table.addMap(concepts::ResultsTable::INT, "iterations", output);
    table.addMap(concepts::ResultsTable::DOUBLE, "space_time", output);
    table.addMap(concepts::ResultsTable::DOUBLE, "stiff_time", output);
    table.addMap(concepts::ResultsTable::DOUBLE, "solve_time", output);

    // ********************************************************** input data **
    std::string inputfile;
    int opt;
    while ((opt = getopt(argc, argv, "-f:l:p:g")) != EOF)
      switch(opt) {
      case 'l': input.addInt("level", std::atoi(optarg)); break;
      case 'p': input.addInt("polynomial", std::atoi(optarg)); break;
      case 'f': inputfile = std::string(optarg);
        inputParser.parse(inputfile);
        break;
      case 'g': input.addBool("graphics", true); break;
      default:
        std::cout << "Usage: " << argv[0] 
                  << " [-f FILE] [-l LEVEL] [-p DEGREE] [-d]"
                  << std::endl
                  << "where" << std::endl
                  << "  FILE: name of the input file" << std::endl
                  << "  LEVEL: level of refinement" << std::endl
                  << "  DEGREE: polynomial degree" << std::endl
                  << "  -g: graphics of solution" << std::endl
                  << "Options given after the input file override the values "
                  << "read from the"
                  << std::endl << "input file." << std::endl;
        std::exit(1);
        break;
      }

    // ************************************************* boundary conditions **
    concepts::BoundaryConditions bc;
    for (int i = 1; i <= input.getInt("numberbc"); ++i) {
      bc.add(concepts::Attribute(i),
             concepts::Boundary((concepts::Boundary::boundaryTypes)
                                input.getArrayInt("bctype", i),
                                concepts::ParsedFormula<>
                                (input.getArrayString("bcform", i).c_str())));
    }

    // ***************************************************** show parameters **
    std::cout << '[' << argv[0] << "]" << std::endl;
    std::cout << "--" << std::endl;
    std::cout << "Parameters:" << std::endl
              << "  input file = " << inputfile << std::endl
              << input;
    std::cout << "--" << std::endl;
    std::cout << bc << std::endl;
    std::cout << "--" << std::endl;

    // ******************************************************** computations **
    fem(input, bc, output);

    // ************************************** output of input data and other **
    std::ofstream* ofs = new std::ofstream(input.getString("gnuplot").c_str());
    *ofs << std::setprecision(20);
    table.print<concepts::ResultsTable::GNUPLOT>(*ofs);
    delete ofs;

    std::cout << "--" << std::endl;
    std::cout << output << std::endl;
    std::cout << table << std::endl;
    std::cout << "--" << std::endl
              << "Writing gathered data to disk: " 
              << input.getString("parameterout") << std::endl;

    ofs = new std::ofstream(input.getString("parameterout").c_str());
    *ofs << "/* program:\t" << argv[0] << std::endl
         << " * command:\t";
    for (int i = 0; i < argc; ++i)
      *ofs << argv[i] << " ";
    *ofs << std::endl
         << " * input file:\t" << inputfile << std::endl;
    *ofs << " */" << std::endl << std::setprecision(20) << inputParser;
    delete ofs;
  }
  catch (concepts::ExceptionBase& e) {
    std::cout << e << std::endl;
    return 1;
  }

  return 0;
}
Home | Doxygen Documentation | Tutorials | Developer Tools (restricted)